Предмет: Математика,
автор: alisa162013
найти общее решение дифференциального уравнения
Приложения:
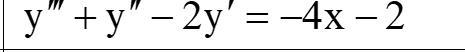
Ответы
Автор ответа:
0
Ответ:
1.
2.
общее решение:
Похожие вопросы
Предмет: Русский язык,
автор: русский3кл
Предмет: Окружающий мир,
автор: ршрошллшош
Предмет: Русский язык,
автор: ласковая2101
Предмет: Биология,
автор: maxsalers
Предмет: Литература,
автор: alina24682