Question

ПОМОГИТЕ,ПОЖАЛУЙСТА!!!ПОДРОБНО.Диагонали ромба относятся как 3 : 4. Вычислите периметр ромба, если известно, что его площадь равна 96 см^2
Только не с интернета,а кто сам понимает

.

Answer 1

Ответ:

Р=40см

Объяснение:

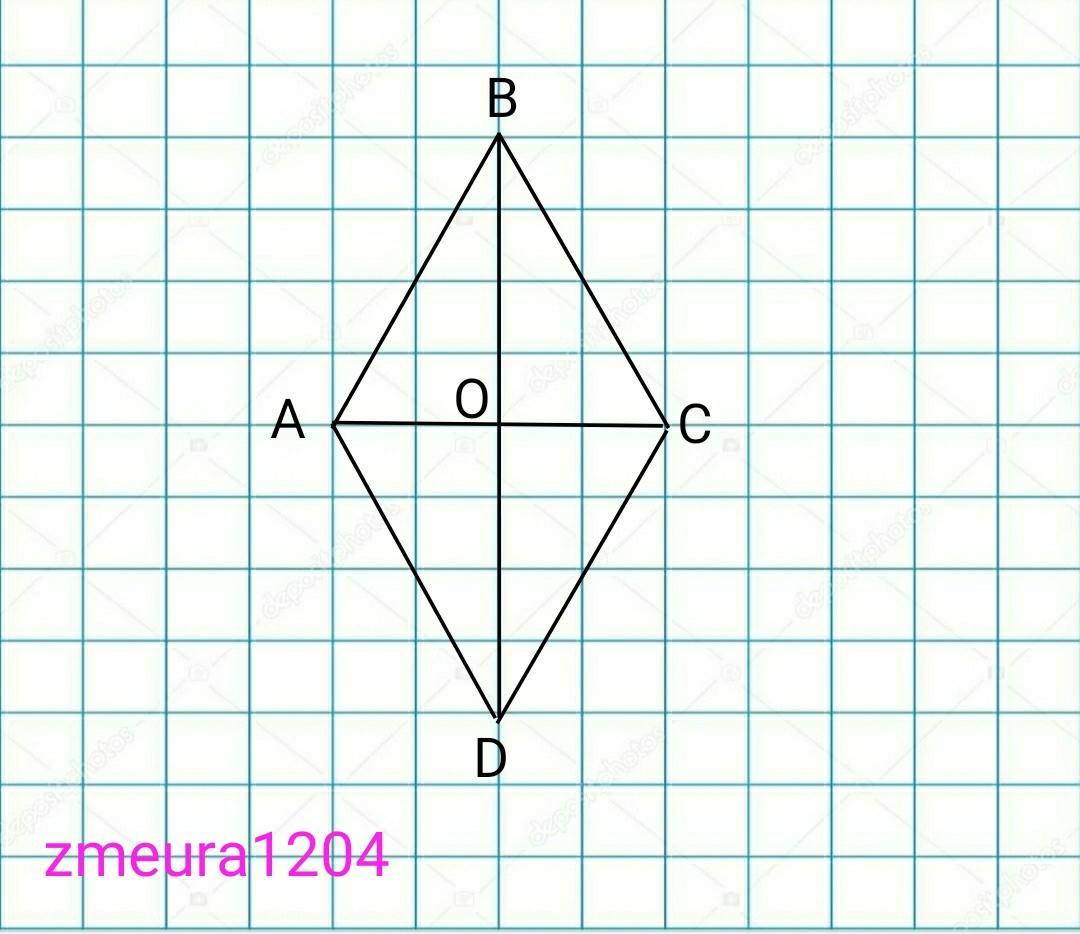
Пусть АС=3х см

ВD=4x см.

S=1/2*AC*BD.

Составляем уравнение

3х*4х=96*2

12х²=192

х²=192/12

х=√16

х=4 только положительный корень

АС=3*4=12 см

ВD=4*4=16 см

Диагонали ромба пересекаются перпендикулярно и точкой пересечения делятся пополам.

АО=АС/2=12/2=6см

ВО=BD/2=16/2=8см

∆АОВ- прямоугольный треугольник.

По теореме Пифагора

АВ=√(АО²+ВО²)=√(6²+8²)=10см.

Р=4*АВ=4*10=40см

Answer 2

Ответ:P=40cm

Объяснение:  пусть наибольшая диагональ равна 4x а наименьшая 3x  площадь  ромба через диагонали равна S=1/2*d1*d2 подставим 1/2*4x*3x=96  =>   6x^2=96  тогда x=4  тогда d1=12 ;d2=16 и есть такая формула $d1^2+d2^2=4a^2$ (это формула верна также для параллелограмма выглядит она так $d1^2+d2^2=2(a^2+b^2)$  где a и b стороны параллелограмма)   где а длина стороны ромба теперь подставим$12^2+16^2=4a^2=>a^2= \frac{256+144}{4}$  тогда а=10 а периметр это 4a=40