Предмет: Геометрия,
автор: sksuhaks
ПОМНИТЕ РАДИ БОГА СРОЧНО
Приложения:
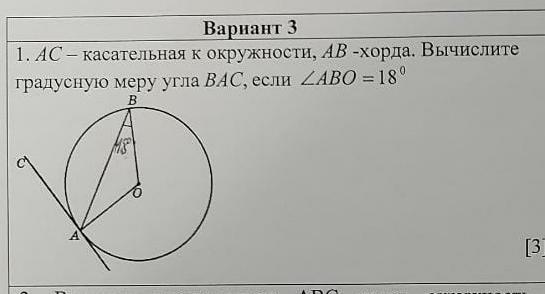
Ответы
Автор ответа:
1
Ответ:
уг. ВАС = 72°
Объяснение:
Рассм. ∆АОВ:
Сторона ОА, и сторона ОВ - радиус окружности
=> OA = OB =>
=> ∆АОВ - равнобедренный с основанием АВ,
т.к. у равнобедр. ∆-ка углы при основании равны =>
=> уг. АВО = уг.ВАО = 18°
Касательная всегда перпендикулярна радиусу окружности, проведенному к точке касания:
АС _|_ ОА, т.е. уг.САО = 90°
уг.САО = уг.ВАО + уг.ВАС =>
=> уг.ВАС = уг.САО - уг. ВАО
уг.ВАО = 18°, уг.САО = 90° =>
=> уг.ВАС = 90 - 18 = 72°
Ответ: уг.ВАС = 72°
Автор ответа:
1
Ответ:
∠ВАС = 72°
Объяснение:
Дано:
∠АВО = 18°
АО = ВО (радиусы окружности)
∠САО = 90° (АС - касательная, АО - радиус)
Найти:
∠ВАС
Решение:
∠ВАО = ∠АВО = 18 °, так как ΔАВО равнобедренный
∠ВАС = ∠ САО - ∠ВАО = 90° - 18° = 72°
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Русский язык,
автор: shckanovaanast
Предмет: Английский язык,
автор: nikolayvazhnov
Предмет: Русский язык,
автор: ПолинаКошкаГейм
Предмет: Русский язык,
автор: Давид46832