Question

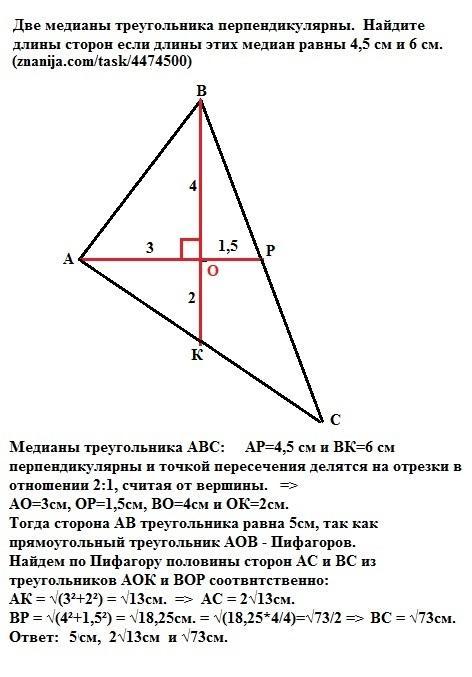
две медианы треугольника перпендикулярны .Найдите длины сторон если длины этих медиан равны 4,5 см и 6 см

Answer 1

Медианы треугольника АВС: АР=4,5 см и ВК=6 см перпендикулярны и точкой пересечения делятся на отрезки в отношении 2:1, считая от вершины.   =>

АО=3см, ОР=1,5см, ВО=4см и ОК=2см.

Тогда сторона АВ треугольника равна 5см, так как прямоугольный треугольник АОВ - Пифагоров c катетами 3см и 4 см.

Найдем по Пифагору половины сторон АС и ВС из прямоугольных треугольников АОК и ВОР соотвнтственно:

АК = √(3²+2²) = √13см.  =>  AC = 2√13см.

ВР = √(4²+1,5²) = √18,25см. = √(18,25*4/4)=√73/2 => ВC = √73см.

Ответ: 5см,  2√13см  и √73см.