Question

80 баллов - Помогите пожалуйста, срочно:
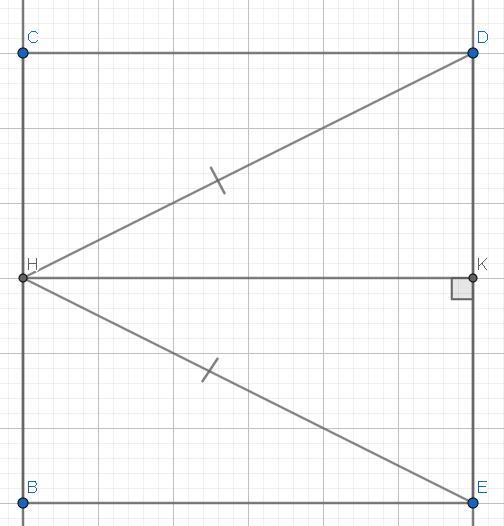
Дан параллелограмм ABCD, в котором из середины его стороны BC точки H проведены два отрезка к вершинам противоположной стороны. Докажи, что все углы этого параллелограмма равны между собой, если указанные отрезки равны.
Моя учительница может придраться ко всему, так что лучше доказывать более менее понятна...

Answer 1

Отезки HD & HE — равны, и также проведены с середины стороны CB.

Точка H  — делит сторону CB пополам, то есть: $CH \equiv HB.$

Треугольники CDH & HEB — равны. Не поверите? Сейчас объясню:

Так как: (HD ≡ HE); (CH ≡ HB); (CD ≡ BE (так как стороны ромба — равны)), то по третьему признаку равенства треугольников: ΔCHD ≡ ΔHBE.

Так как отрезки HD & HE — равны, то треугольник EHD — равнобедренный.

Проведём с вершины, противоположной основанию(точка H) — медиану: отрезок HK.

Теперь: DK ≡ KE.

И так как треугольник — равнобедренный, то: высота, медиана, и биссектриса, проведённая с вершины, противоположной основанию — одно и то же.

То есть: HK — высота, которая образует 2 прямоугольник треугольника: ΔHKE & ΔHDK.

Эти треугольники друг другу равны по трём сторонам: (DK ≡ KE); (HD ≡ HE); (HK — общая).

Так же: ΔCHD = ΔHEB = ΔHKE = ΔHDK, опять же: по трём сторонам.

Что и означает, что: ΔHCD &  HBE — прямоугольные, и так как ABCD  —ромб, то: $<B = <C \Rightarrow <B = <C = <A = <D.$

То есть: соседные углы равны, что и означает, что: $<A = <B = <C = <D = 360/4 = 90^o.$

И так как ромб — имеет равны стороны, то: ABCD = квадрат.