Предмет: Геометрия,
автор: Hukiiss
СРОЧНО!
Даны вершины треугольника ABC : A(1; 2;3) , B(4; -10; 7),
С(3;-1;9).
Найти: Середину отрезка СВ. Найти медиану АД. Площадь
треугольника АВС.
Sakaido:
как много времени есть?
могу оформить полностью, или только принцип решения
Извините за игнор.Времени +-2-3 часа
Как вам удобно будет ^^
Я все-таки решил сделать полное решение
Ответы
Автор ответа:
1
Дано:
∆ABC
A(1;2;3)
B(4;-10;7)
C(3;-1;9)
Найти:
середину отрезка CB
Медиану AD
площадь ∆ABC
Решение:
Пусть точка D лежит на середине отрезка CB, тогда справедливы равенства
Dx = (Cx + Bx)/2
Dy = (Cy + By)/2
Dz = (Cz + Bz)/2
Подставим известные нам величины
Dx = 3.5
Dy = -5.5
Dz = 8
То середина отрезка CB имеет координаты D(3.5;-5.5;8)
Медиана AD имеет длину, равную
Таким же образом находим длины сторон треугольника
Воспользуемся формулой Герона
Ответ: D(3.5;-5.5;8) ; ;
Внизу приложил как точки располагаются в пространстве
Приложения:
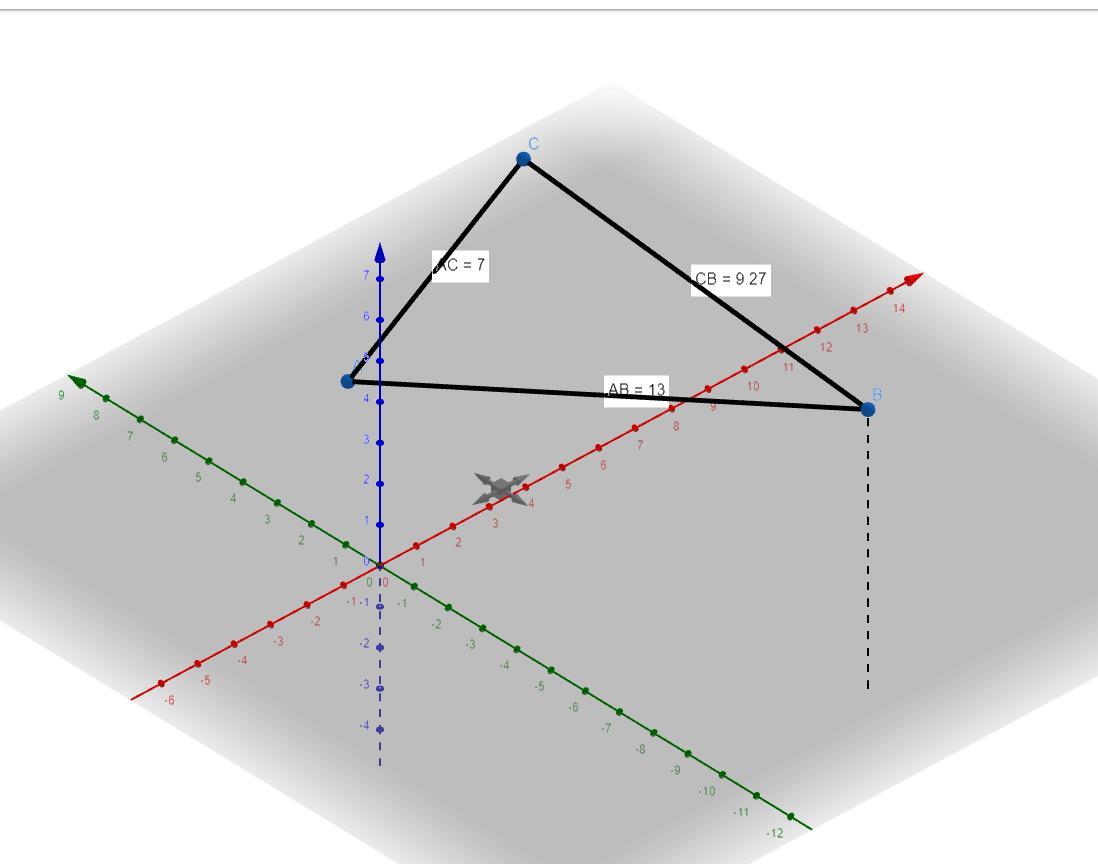
Спасибо!
Похожие вопросы
Предмет: Физика,
автор: Magistor15
Предмет: Английский язык,
автор: Софья551
Предмет: Химия,
автор: Викундель749
Предмет: История,
автор: olegchudnov
Предмет: Русский язык,
автор: mbs6012