Предмет: Геометрия,
автор: jdjsjdjxnxhxhx
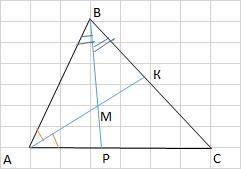
Биссектрисы углов A и B треугольника ABC пересекаются в точке M.
Найдите ∠C, если ∠AMB = 126⁰.
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Биссектрисы углов делят их пополам.
Рассмотрим ΔАМВ.
∠АМВ = 126°. Т.к. сумма всех углов треугольника = 180°, то
∠ВАМ + ∠АВМ = 180° - 126° = 54°
Но ∠ВАМ = ½∠А, т.к. АК - биссектриса ∠А, а
∠АВМ = ½∠В, т.к. ВР - биссектриса ∠В. Тогда
½∠А + ½∠В = 54°
(∠А + ∠В) : 2 = 54° → ∠А + ∠В = 54° * 2 = 108°
Рассмотрим ΔАВС
∠А + ∠В + ∠С = 180°
∠С = 180° - ((∠А + ∠В) = 180° - 108° = 72°
Ответ: ∠С = 72°
Приложения:
Похожие вопросы
Предмет: Математика,
автор: настяlove2
Предмет: Окружающий мир,
автор: olena21
Предмет: География,
автор: funikova1998
Предмет: Математика,
автор: andrei1234567892
Предмет: Алгебра,
автор: KILLER1465