Question

Решите срочно пожалуйста полностью дз!!! За ответы по типу "вовьалл" "скоро решу" "1+1=0" Даю бан​​

Answer 1

1) ОФ это радиус первой(большей) окружности

ОF+ОD=12    ⇒ OF=12-OD

DF=6

OF=OD+DF подставим значение OF

12-OD=OD+6

2OD=12-6

2OD=6

OD=6/2=3 это радиус меньшей окружности, теперь найдем

OF=12-OD=12-3=9

2)внутр.касание 11-7=4

внеш=11+7=18

3)

1. да(6+4=10 а расстояние между центрами 9)  
2. Касаются друг друга(4,5+4,5=9)  
3. нет(2+6=8 меньше 9)

Answer 2

Ответ:

1. R = 6 см, r =3 см

2.

2.1: О1О2 = 4 см

2.2: О1О2 = 18 см

3.

3.1: пересекаются, 2 т. пересечения

3.2: пересекаются (касаются) 1 т. пересечения

3.3: не пересекаются, общих точек нет

Объяснение:

1.

Дано:

Окружности (О;r) и (О;R)

т.О - общая; ОD = r, OF = R

R + r = 12 см; I = 6 см

Найти:

R = ?; r = ?

Решение:

т.к. ОD = r, OF = R =>

=> ОF + OD = 12 см =>

=> R + r = 12 см;

DF = ОF - OD = 6 см =>

=> R - r = 6см

Получаем систему

$\small{\begin{cases}R+r=12 \\ R-r = 6 \end{cases} < = > \begin{cases}R=12 - r\\ R= 6 + r\end{cases} < = > } \\ \small{\begin{cases}6{+}r{=}12{ -} r \\ R= 6 + r \end{cases}{ <} {= }{ > }\begin{cases}2r=6 \\ R= 6 {+ }r \end{cases}{ < }{ =}{ > }\begin{cases}r{=}3 \\ R{= }9 \end{cases}}$

Ответ: R = 9 см, r = 3 см

2.

Дано:

окружности

$(O_1; R_1), R_1 = 7 \: cm \\ (O_2; R_2), R_2 = 11 \: cm$

касаются друг друга, т.е. имеют единственную общую точку D:

$D\in(O_1; R_1) ; \: \: D\in(O_2; R_2)$

Найти:

$O_1O_2=?$

Решение 1: внутреннее касание (см.рис.):

Окружности касаются внутренним образом, окружность (О1; R1) полностью находится внутри (O2; R2) при этом расстояние между центрами окружностей равно разности их радиусов:

$O_1O_2=R_2 - R_1 \\ O_1O_2=11 - 7 = 4 \: cm$

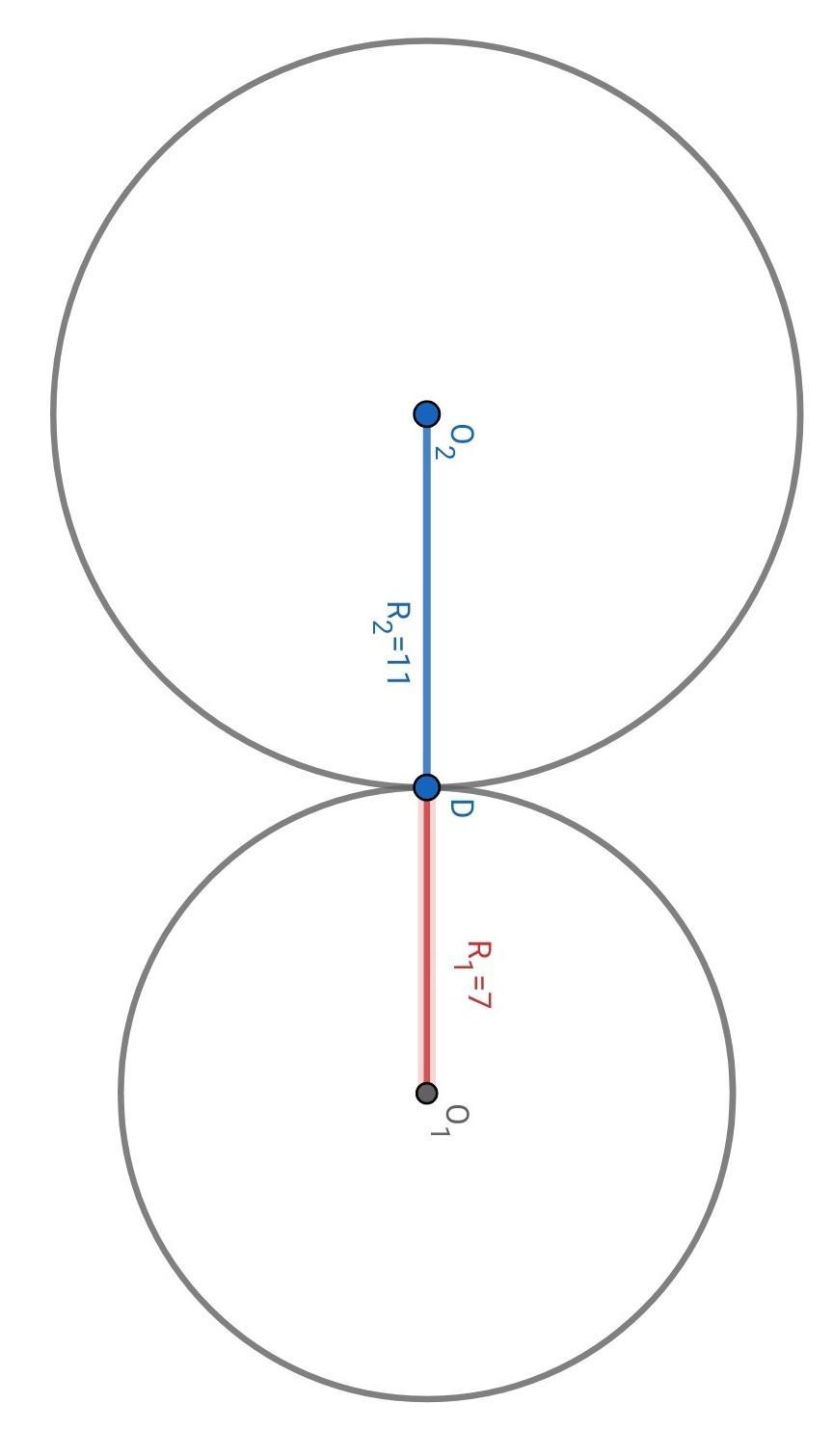
Решение 2: внешнее касание (см.рис.):

Окружности касаются внешним образом, находятся по разные стороны от касательной в точке D. И при этом расстояние между центрами окружностей равно сумме их радиусов:

$O_1O_2=R_2 + R_1 \\ O_1O_2=11 + 7 = 18 \: cm$

3.

Дано:

окружности

$(O_{1};R_{1}), \:(O_{2};R_{2})\\ O_1O_2=9 \:cm$

Определить:

Пересекаются ли окружности с радиусами

$1) \:R_{1}=6, R_{2}=4 \:cm\\ R_1+R_2=6+4=10>O_1O_2$

- да. Окружности пересекаются и имеют 2 точки пересечения, т.к. сумма радиусов больше расстояния между центрами

$R_{1}=4,5, R_{2}=4,5 \:cm\\ R_1+R_2=4,5+4,5=9=O_1O_2$

= - да. Окружности касаются друг друга и имеют 1 общую точку, т.к. сумма радиусов равна расстоянию между центрами

$R_{1}=2, R_{2}=6\:cm\\ R_1+R_2=2+6=8<O_1O_2$

- нет. Окружности не пересекаются и не имеют общих точек, т.к. сумма радиусов меньше расстояния между центрами