Question

помогите мне кто-нибудь В94. ​

Answer 1

Ответ:

Пошаговое объяснение:

критические точки ищем при помощи первой производной

$\displaystyle y' = 3^{(-0.3x^2+1.8x+1.3)}(-0.6x+1.8)ln(3)$

$\displaystyle 3^{(-0.3x^2+1.8x+1.3)}(-0.6x+1.8)ln(3) = 0 \Rightarrow (-0.6x+1.8)=0\Rightarrow x=3$

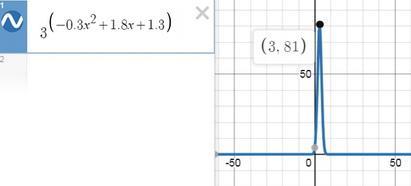
есть одна критическая точка х0 = 3

у(3) = 81

теперь надо узнать - это минимум или максимум

для этого берем достаточное условие экстремума.

вторая производная

$\displaystyle y'' = 3^{(-0.3x^2+1.8x+1.3)}(-0.6x+1.8)^2ln^2(3)-0.6*3^{(-0.3x^2+1.8x+1.3)}ln(3)$

теперь считаем

y''(3) ≈ -53  <  0 - значит точка x0 = 3 точка максимума функции

ответ

наибольшее значение функции достигается в точке х0 =3 и равно

y(3) = 81