Помогите пожалуйста полный ответ
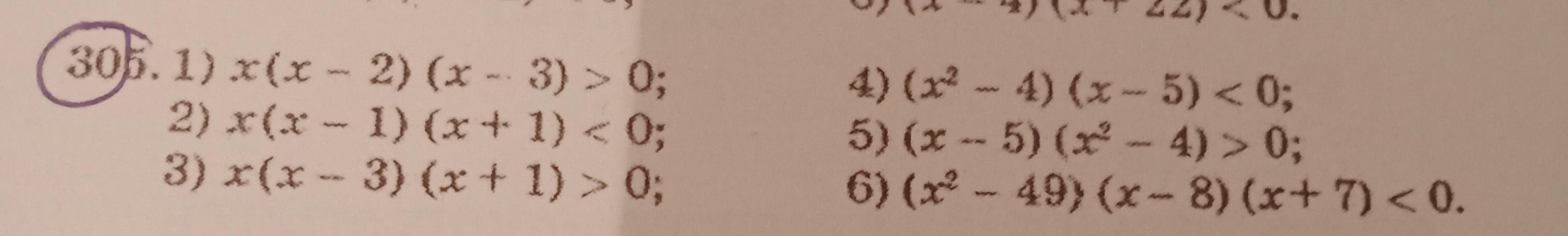
Ответы
Ответ:
В решении.
Объяснение:
Решить неравенство:
1) х(х - 2)(х - 3) > 0
Приравнять к нулю, разложить на множители, каждый сомножитель приравнять к нулю и определить значение корней:
х(х - 2)(х - 3) = 0
х₁ = 0;
х - 2 = 0; х₂ = 2;
х - 3 = 0; х₃ = 3.
Начертить числовую прямую, отметить на ней все корни:
_______________________________________________
- 0 + 2 - 3 +
Определить знак самого правого интервала, для этого придать х любое значение, больше 3 и подставить в уравнение:
х = 4;
4 * 2 * 1 = 8 >0, значит, знак плюс.
Влево знаки меняются через корень.
Так как неравенство > 0, решениями будут интервалы со знаком плюс:
Решения неравенства: х∈(0; 2)∪(3; +∞).
2) х(х - 1)(х + 1) < 0 Решение по той же схеме:
х(х - 1)(х + 1) = 0
х₁ = 0;
х - 1 = 0; х₂ = 1;
х + 1 = 0; х₃ = -1.
________________________________
- -1 + 0 - 1 +
х = 2;
2 * 1 * 3 = 6 > 0, значит, плюс.
Так как неравенство < 0, решениями будут интервалы со знаком минус:
Решения неравенства: х∈(-∞; -1)∪(0; 1).
3) х(х - 3)(х + 1) > 0 Решение по той же схеме:
х(х - 3)(х + 1) = 0
х₁ = 0;
х - 3 = 0; х₂ = 3;
х + 1 = 0; х₃ = -1.
______________________________
- -1 + 0 - 3 +
х = 4;
4 * 1 * 5 = 20 > 0, значит, знак плюс.
Так как неравенство > 0, решениями будут интервалы со знаком плюс:
Решения неравенства: х∈(-1; 0)∪(3; +∞).
4) (х² - 4)(х - 5) < 0 Решение по той же схеме:
(х² - 4)(х - 5) = 0
(х - 2)(х + 2)(х - 5) = 0
х - 2 = 0; х₁ = 2;
х + 2 = 0; х₂ = -2;
х - 5 = 0 х₃ = 5.
_____________________________________
- -2 + 2 - 5 +
х = 6;
(36 - 4)(6 - 5) = 32 > 0, значит, знак плюс.
Так как неравенство < 0, решениями будут интервалы со знаком минус:
Решения неравенства: х∈(-∞; -2)∪(2; 5).
5) (х - 5)(х² - 4) > 0 Решение по той же схеме:
(х - 5)(х² - 4) = 0
(х - 5)(х - 2)(х + 2) = 0
х - 5 = 0; х₁ = 5;
х - 2 = 0; х₂ = 2;
х + 2 = 0; х₃ = -2.
_________________________________
- -2 + 2 - 5 +
х = 6
(6 - 5)(36 - 4) = 32 > 0, знак плюс.
Так как неравенство > 0, решениями будут интервалы со знаком плюс:
Решения неравенства: х∈(-2; 2)∪(5; +∞).
6) (х² - 49)(х - 8)(х + 7) < 0 Решение по той же схеме:
(х² - 49)(х - 8)(х + 7) = 0
(х - 7)(х + 7)(х - 8)(х + 7) = 0
х - 7 = 0; х₁ = 7;
х + 7 = 0; х₂ = -7;
х - 8 = 0; х₃ = 8;
х + 7 = 0; х₄ = -7.
__________________________________
- -7 + 7 - 8 +
х = 9;
(81 - 49)(9 - 8)(9 + 7) = 512 > 0, знак плюс.
Так как неравенство < 0, решениями будут интервалы со знаком минус.
Решения неравенства: х∈(-∞; -7)∪(7; 8).
Проверить выполнение неравенства при х < -7, в решении два одинаковых корня. Придать х значение -8 и подставить в уравнение:
х = -8;
(64 - 49)(-16)(-1) = 240 > 0, неравенство не выполняется.
Значит, решение неравенства: х∈(7; 8).