Предмет: Геометрия,
автор: fihjk
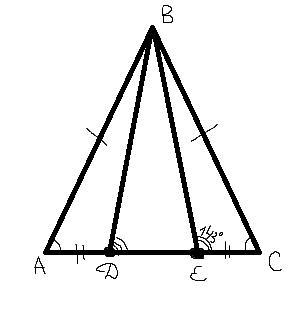
Дан равнобедренный треугольник ABC с боковыми сторонами AB=BC. На основании расположены точки D и E так, что AD=EC, ∡CEB=143°. Определи ∡EDB.
Ответы
Автор ответа:
1
1) Рассмотрим ΔАDB и ΔBEC. АВ=ВС, АD=EC по условию, ∠А= ∠С как углы при основании равнобедренного треугольника. Значит ΔABD= ΔBEC по двум сторонам и углу между ними. Из равенства треугольников следует, что ∠BEC=∠BDA=143°.
2) ∠EDB=180°-∠BDA=180°-143°=37° как смежные углы.
Ответ: ∠EDB=37°.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Марина193006
Предмет: Английский язык,
автор: maksundr1
Предмет: Русский язык,
автор: Nastiklove1
Предмет: Математика,
автор: Edison88
Предмет: Физика,
автор: marinaslavik