Предмет: Алгебра,
автор: fifala9202
Откуда взялась формула, которая подчеркнута? Почему числитель и знаменатель поменяли местами?
То, что написано ниже - попытки получить ту же формулу, которые, к сожалению, были неудачными.
Приложения:
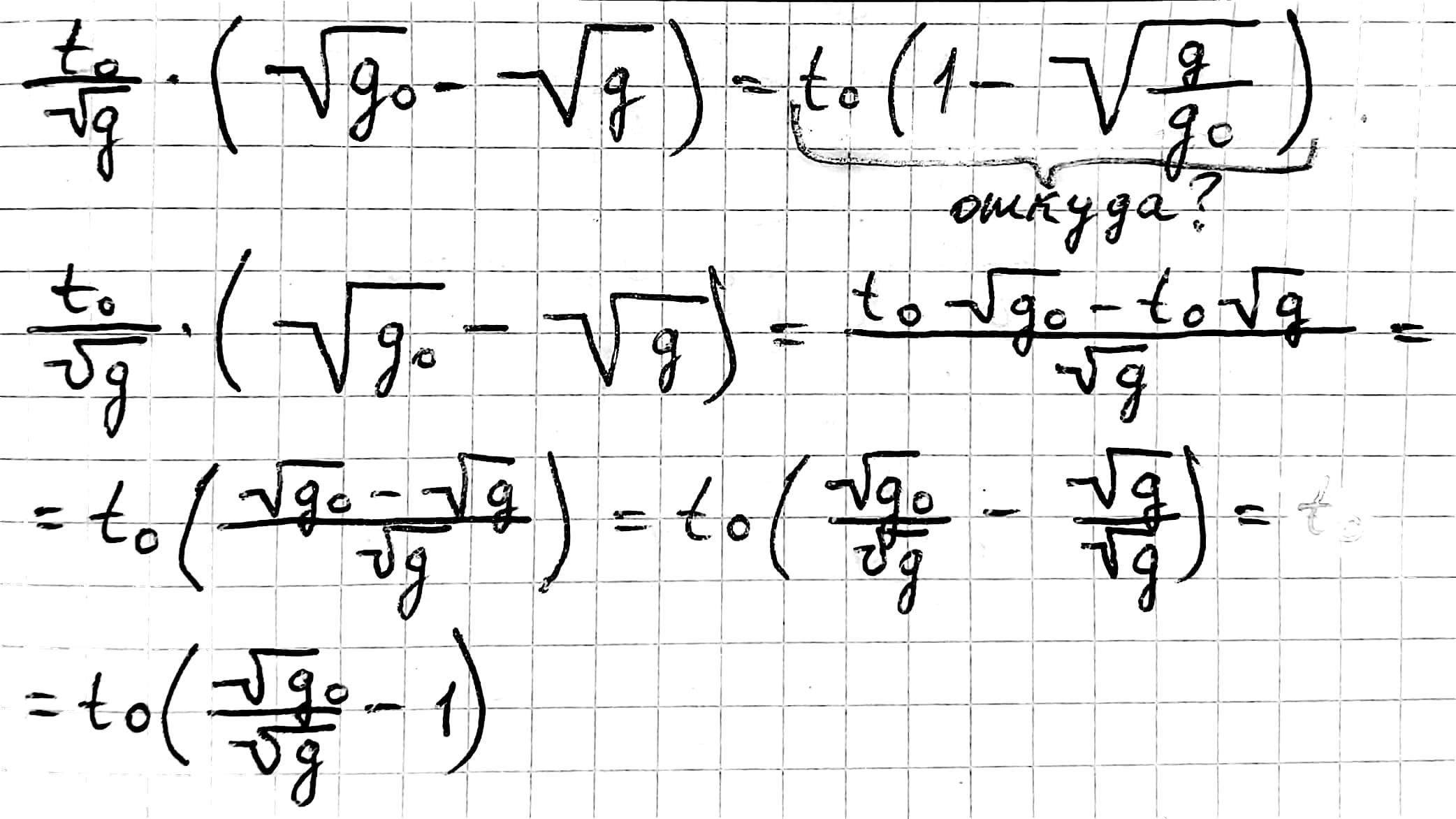
Ответы
Автор ответа:
1
Ответ:
В формуле пропущен знак минус .
Если бы было выражение вот такое:
fifala9202:
Да, я тоже думал о таком решении. Мы t с минусом можем вынести, тогда всё сойдётся. Мне встретилось это в решении задачи по физике. Думаете, там минус пропущен, т.к. время не может быть меньше 0?
Так ещё числитель и знаменатель перевернуты по какой-то причине.
минус точно пропущен , но так как время не может быть меньше 0, то (-t0) умножается на скобку, которая сама <0 , то есть произведение положительно, когда оба множителя одного знака .
ещё может быть то, что вы упустили 0 в знаменателе первой дроби, то есть в знаменателе стоит не sqrt(g) , a sqrt(g0) ...
Спасибо огромное. Пойду, наверное, задам вопрос злой учительнице, которая будет орать и говорить о том, что параллельный класс всегда умнее!)
если бы в знаменателе 1 дроби стояло sqrt(g0) , то получилось бы выша формула t_0(1-sqrt(g/g0) ...
Похожие вопросы
Предмет: Русский язык,
автор: asirlis
Предмет: Русский язык,
автор: bektoj777
Предмет: Английский язык,
автор: salihasalykova
Предмет: Алгебра,
автор: lerako2001
Предмет: Математика,
автор: lexus9