Предмет: Алгебра,
автор: Аноним
Упростите тригонометрическое выражение (8;9;10)
(тема: Тождественные преобразования тригонометрических выражений)
Приложения:
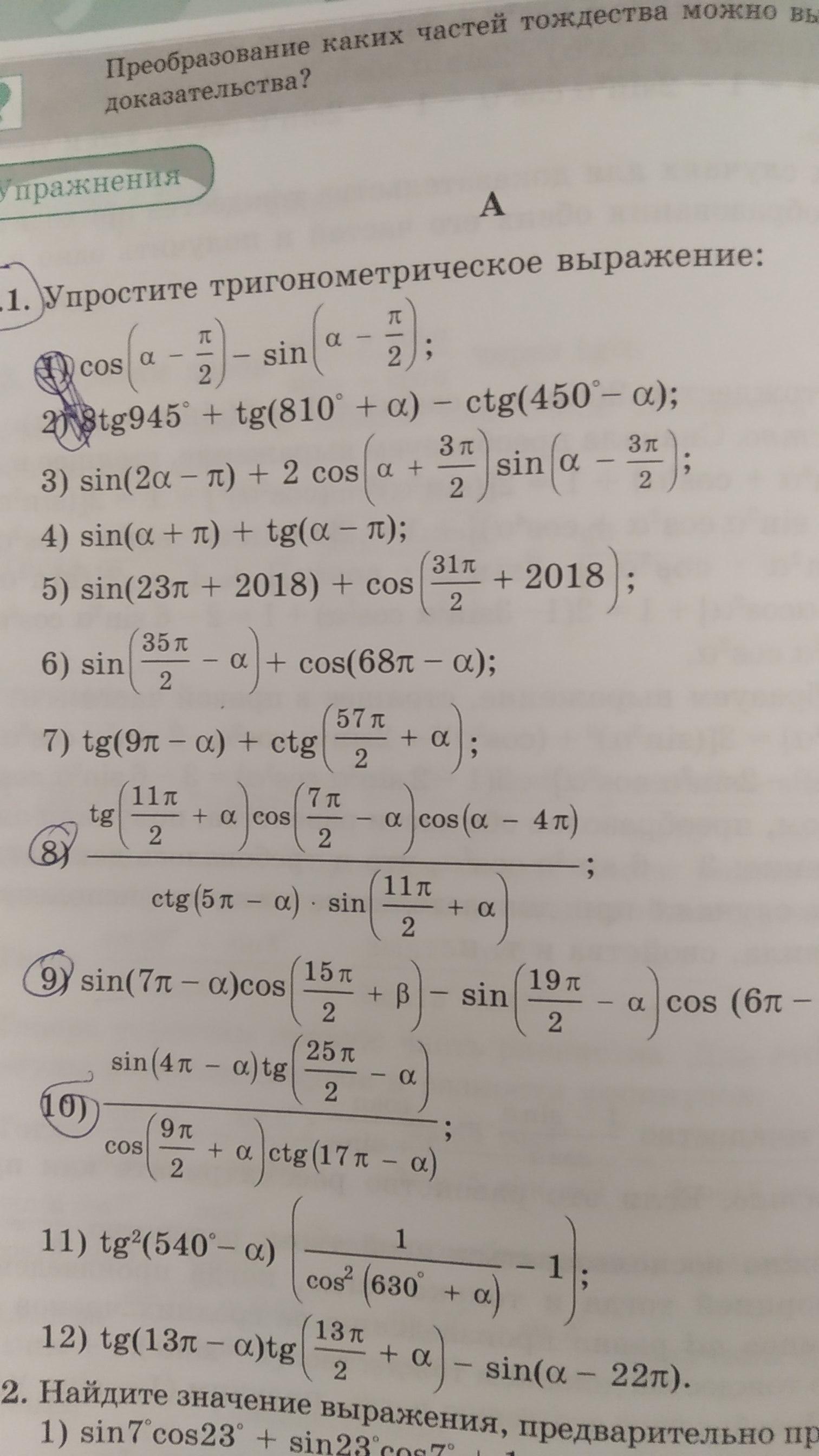
Ответы
Автор ответа:
3
8
9
10
Автор ответа:
0
Ответ:
Объяснение:
См. в приложении
Приложения:


Похожие вопросы
Предмет: Русский язык,
автор: polkamicu
Предмет: Қазақ тiлi,
автор: 3456789012345
Предмет: Русский язык,
автор: kadriya1988
Предмет: Физика,
автор: дашаааа5