Предмет: Математика,
автор: NIXXKARMA
Решите пожалуйста, даю 10 баллов
Приложения:
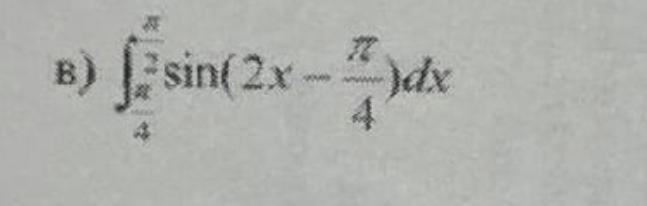
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
1)
2)
Похожие вопросы
Предмет: Русский язык,
автор: Raxman775
Предмет: Қазақ тiлi,
автор: Saule789
Предмет: Русский язык,
автор: shestopala18
Предмет: Математика,
автор: evaava098
Предмет: Математика,
автор: DimaWolk