Предмет: Математика,
автор: evaava098
log4(16x^4)+11/log^2 4(x)-9≥-1
Приложения:
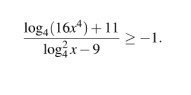
Ответы
Автор ответа:
6
одз
{x>0
{x≠64
{x≠1/64
+++++(1/64)-----------[1/16]---------(64)
x∈(-∞;1/64)U{1/16}U(64;+∞)
с учетом одз получаем ответ
x∈(0;1/64)U{1/16}U(64;+∞)
evaava098:
а можете написать из чего следует 64 и 1/64, пожалуйста?
4^3=64;4^(-3)=1/64
спасибо
если заменить на t, одз можео не писать?
Похожие вопросы
Предмет: Физика,
автор: ASFADFAFAF
Предмет: Математика,
автор: polinaklem113
Предмет: Математика,
автор: arinakostrytsia
Предмет: Алгебра,
автор: влада89221954838
Предмет: Обществознание,
автор: maksimka2001768