Предмет: Алгебра,
автор: Darvin2004
Помогите решить задание из тригонометрии
Приложения:
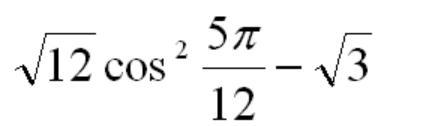
Ответы
Автор ответа:
0
Ответ:
-1.5
Объяснение:
Darvin2004:
откуда первая строчка взялась? это как?
Формула понижения степени:
cos^2(a/2)=(1+cos(a))/2
cos^2(a/2)=(1+cos(a))/2
Из этой же серии:
sin^2(a/2)=(1-cos(a))/2
tg^2(a/2)=(1-cos(a))/(1+cos(a))
ctg^2(a/2)=(1+cos(a))/(1-cos(a))
sin^2(a/2)=(1-cos(a))/2
tg^2(a/2)=(1-cos(a))/(1+cos(a))
ctg^2(a/2)=(1+cos(a))/(1-cos(a))
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: rufina112
Предмет: Русский язык,
автор: zaika221
Предмет: Другие предметы,
автор: крокодил22