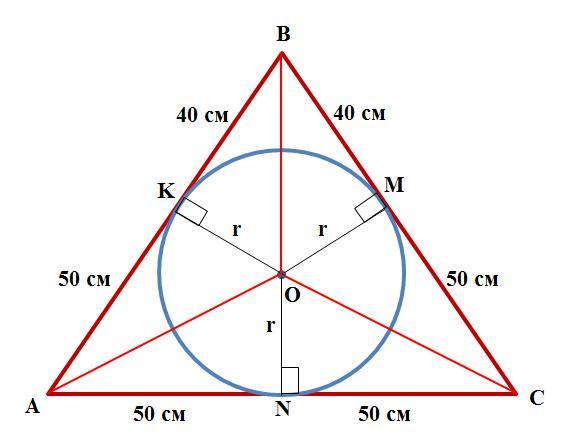
В равнобедренный треугольник ABC с основанием AC вписана окружность. Точка касания окружности и боковой стороны делит сторону на два отрезка: AK = 50 см, BK = 40 см. Найди периметр треугольника ABC.
PΔABC =см.
Ответы
Ответ:
280 см
Объяснение:
Дано (см. рисунок):
ΔABC
AB=BC
AK = 50 см
BK = 40 см
Найти: P(ΔABC) - периметр ΔABC.
Решение. Обозначим через M и N точки касания вписанной окружности со сторонами BC и AC треугольника ABC, О - центр вписанной окружности, r - радиус вписанной окружности. По свойству вписанной окружности радиус r перпендикулярен к сторонам треугольника ABC. Тогда получаем прямоугольные треугольники:
AKO, ANO, BKO, BMO, CMO, CNO.
По условию треугольник ABC равнобедренная и поэтому BK=BM и AK=CM.
Для прямоугольных треугольников:
1) AKO и ANO катеты KO и NO равны, а гипотенуза AO общая;
2) BKO и BMO катеты KO и MO равны, а гипотенуза BO общая;
3) CMO и CNO катеты MO и NO равны, а гипотенуза CO общая.
По признаку равенства прямоугольных треугольников по катету и гипотенузе прямоугольные треугольники AKO и ANO, BKO и BMO, CMO и CNO равны.
Тогда AN=AK=50 см, BM=BK=40 см, CM=CN=AK=50 см.
Далее, определим периметр треугольника ABC:
P(ΔABC)=AB+BC+AC=(AK+BK)+(BM+CM)+(AN+CN)=
=(50+40)+(40+50)+(50+50)=280 см.