Предмет: Геометрия,
автор: vikusia3008
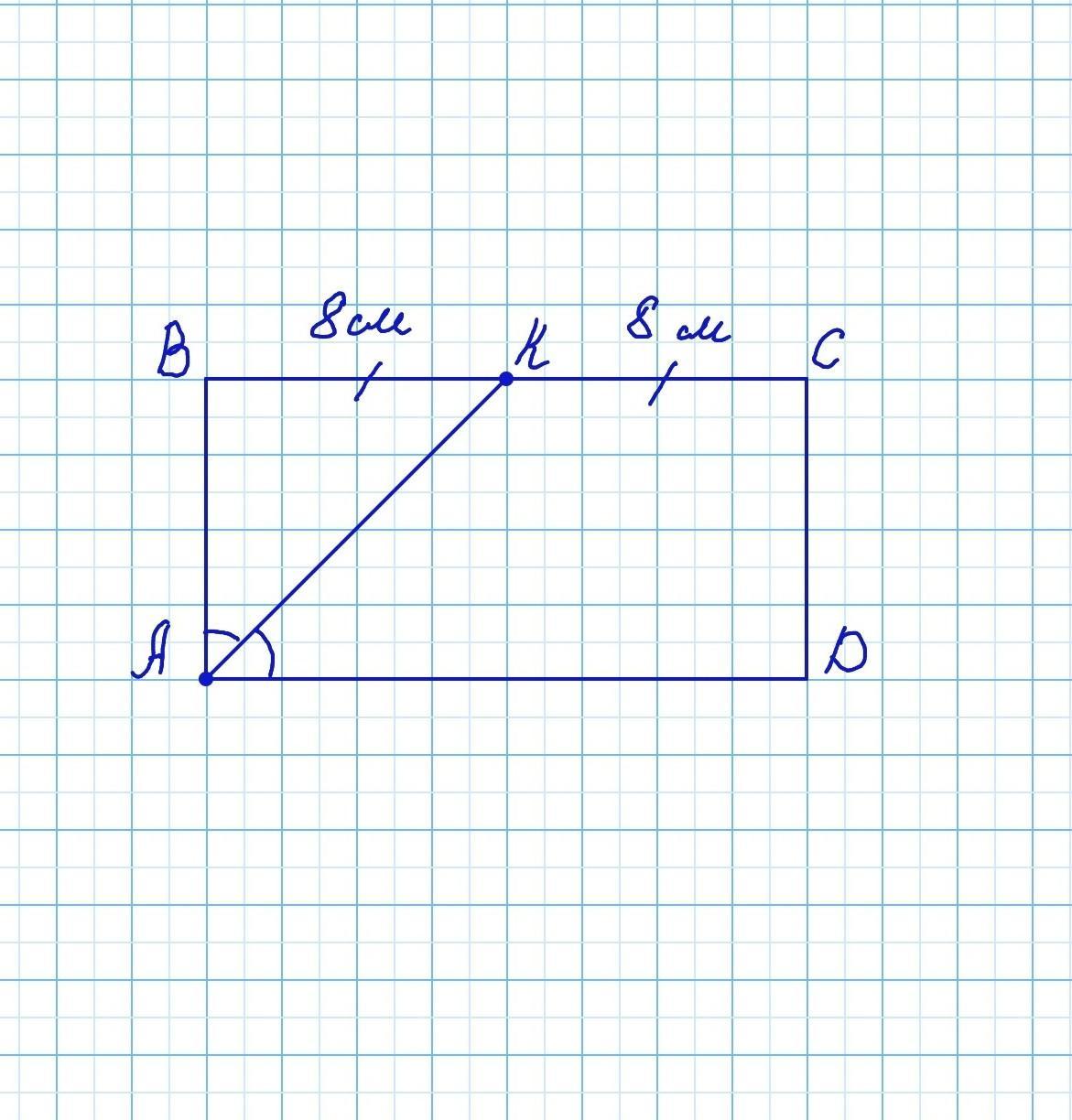
Бісектриса кута А прямокутника ABCD перетинає сторону ВС в точці К.
Обчисліть плошту чотирикутника AKCD, якщо ВК = KC= 8 см
Ответы
Автор ответа:
0
Ответ:
S(AKCD) = 96 см²
Объяснение:
Так как АК – биссектриса, то ∠ВАК=∠DAK.
ABCD – прямоугольник. Следовательно его противоположные стороны равны и параллельны.
Если в прямоугольнике проведена биссектриса, которая пересекает одну из сторон, то она отсекает от прямоугольника равнобедренный треугольник.
Так как ВС║АD, то ∠ВКА=∠DAK – как внутренние накрест лежащие углы при секущей АК.
⇒ ∠ВКА = ∠ВАК.
⇒ΔАВК – равнобедренный. АВ=ВК=8 см
Четырехугольник AKCD является прямоугольной трапецией.
Основание КС=8см, основание АD=ВС=ВК+КС=8+8=16см, высота СD=АВ=8см.
Площадь трапеции находим по формуле:
S(AKCD) = 96 см²
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: nananahel2ex
Предмет: Английский язык,
автор: galina2562
Предмет: Русский язык,
автор: levchikun
Предмет: Физика,
автор: СтарыйМатематик
Предмет: География,
автор: bazuka1312