Question

Около правильного шестиугольника, сторона которого равна 16 см, описан круг. Вычисли площадь круга (π=3,14) (ответ округли до сотых):
Ответ: ? см2.

Определи число сторон выпуклого правильного многоугольника или сделай вывод, что такой многоугольник не существует, если дана сумма всех внутренних углов (если многоугольник не существует, то вместо числа сторон пиши 0):
1. Если сумма углов равна 2430, то многоугольник
(существует/не существует), число сторон — ?.
2. Если сумма углов равна 2340, то многоугольник (существует/не существует), число сторон — ?.

Answer 1

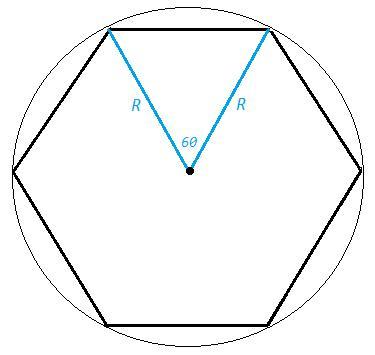
1) Вершины правильного шестиугольника делят окружность на 6 равных дуг, 360/6=60

Соединим две вершины с центром, радиусы равны - равнобедренный треугольник, угол между радиусами 60 - равносторонний треугольник.

Таким образом радиус равен стороне, 16

S круга =пR^2 =3,14 *16^2 =803,84 (см^2)

2) Сумма углов выпуклого n-угольника 180°(n-2)

Понятно, что сумма углов должна нацело делиться на 180.

1. 2430/180 =13,5 => не существует, 0

2. n =2340/180 +2 =15