Question

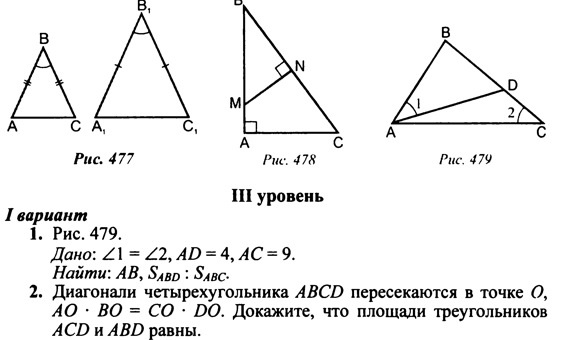
СРОЧНО ПОЖАЛУЙСТА))2)Диагонали четырёхугольника ABCD пересекаются в точке O, AO*BO=CO*DO. Докажите что площади треугольников ACB и ABD равны.1) на картинке Срочно

Answer 1

S(ABD)=S(ABO)+S(AOD), S(ACB)=S(ABO)+S(BOC),
докажем, что площадь треугольника АОД=площади треугольника ВОС
S(AOD)=1/2OA*ODsinAOD
S(BOC)=1/2BO*OCsinBOCугол ВОС=углу АОД как вертикальные, значит и
 sin BOC=sinAOD
по свойству пропорции из АО*ВО=СО*ДО следует АО*ОД=ВО*ОС поэтому S(AOD)=S(BOC)