Предмет: Алгебра,
автор: babin102130
Помогите с интегралами
Приложения:
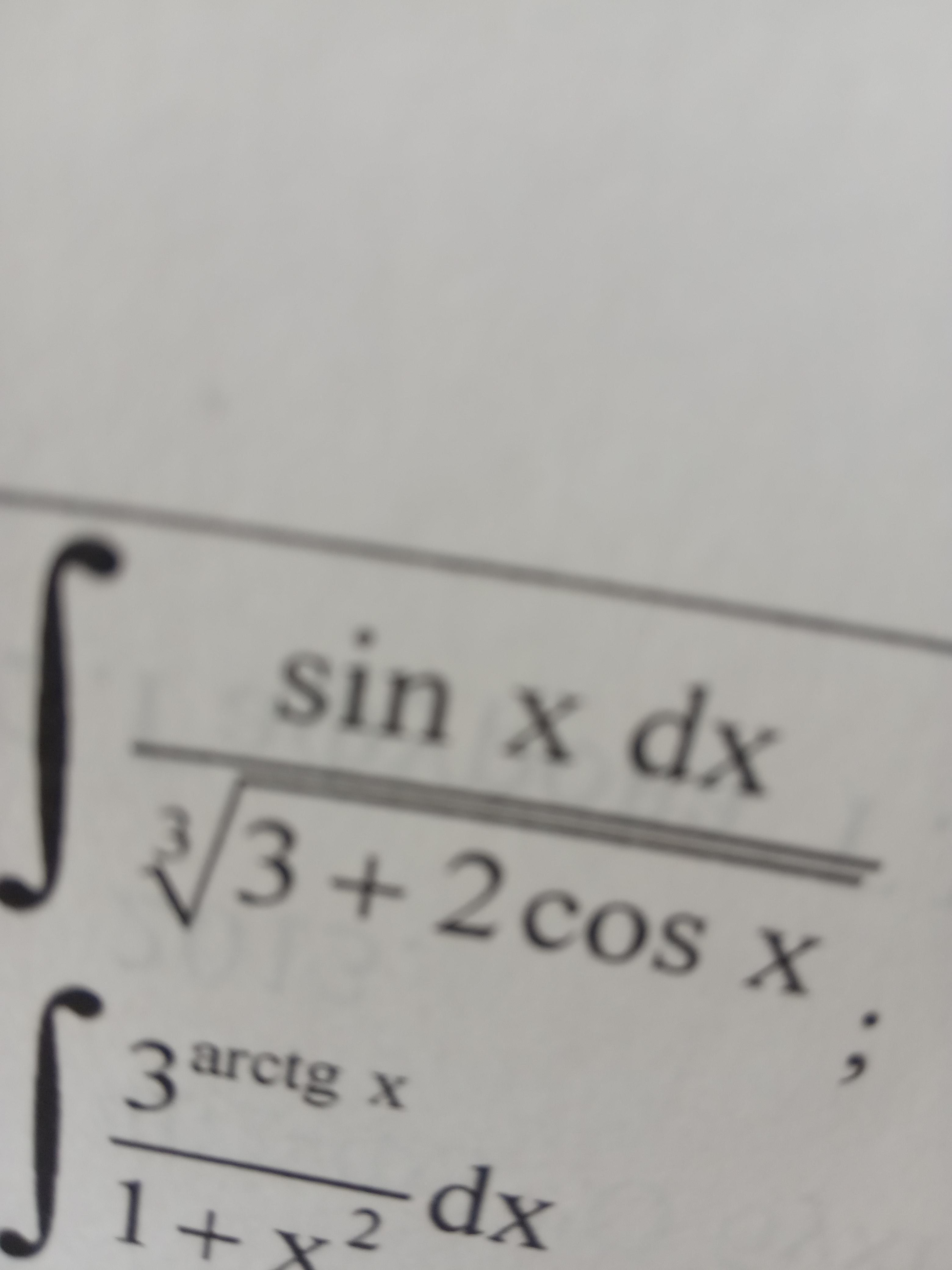
Ответы
Автор ответа:
1
Ответ:
1.
2.
Похожие вопросы
Предмет: Українська література,
автор: Оумен
Предмет: Русский язык,
автор: elenaburova
Предмет: Русский язык,
автор: HunterFridge
Предмет: Биология,
автор: Malena888