Сторона основания правильной треугольной пирамиды равна 240 см, боковое ребро с плоскостью основания образует угол 30°.
Вычисли высоту пирамиды.
Ответ: высота пирамиды равна ... см.
Ответы
Ответ:
OK = 80 см
Объяснение:
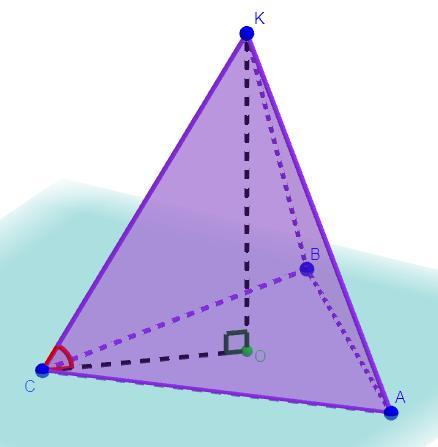
Дано: KABC - правильная пирамида, AB = BC = AC = 240 см,
∠(KC,ABC) = 30°, OK ⊥ ABC
Найти: OK - ?
Решение:
Так как по условию KABC - правильная пирамида, то в основании правильной пирамиды по определению лежит правильный многоугольник, то есть треугольник ΔABC - правильный.
По определению правильной пирамиды высота пирамиды проектируется в центр правильного многоугольника, то есть точка O - центр треугольника ΔABC.
Рассмотрим треугольник ΔABC. По свойствам правильного треугольника все его углы равны 60°, тогда угол ∠ABC = 60°. По следствию из теоремы синусов:
см.
По определению радиуса описанной окружности см.
Рассмотрим треугольник ΔKOC.
Так как по условию OK ⊥ ABC, то треугольник прямоугольный и угол ∠KOC = 90°, следовательно OC - проекция отрезка KC на плоскость ABC, тогда ∠(KC,ABC) = ∠KCO = 30°.
По определению тангенса в прямоугольном треугольнике:
см