Помогитеееееее
Из некоторой точки вершина горы видна под углом 30°. При приближении к горе на 0,5 км вершина стала видна под углом 45°. Найдите высоту горы.
Ответы
Ответ:
Высота горы ≈ 0,683 км ≈ 683 м.
Объяснение:
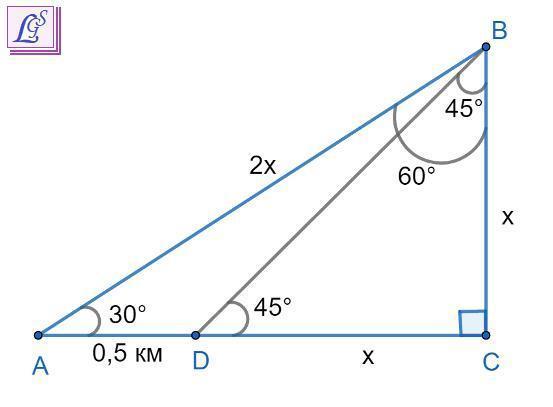
Дано: ΔABC; ВС - высота горы; ∠BAC = 30°; ∠BDC = 45°; AD = 0,5 км.
Найти высоту горы BC.
Решение.
1) Расстоянием от точки до прямой является длина перпендикуляра, опущенного из этой точки на прямую.
⇒ BC⊥AC, ΔABC прямоугольный, ∠С = 90°, высота горы - катет BC.
2) В ΔABC ∠BAC = 30° (по условию), ∠ACB = 90°,
тогда ∠ABC = 180° - 30° - 90° = 60°.
Обозначим для удобства высоту горы катет ВС = x. В прямоугольном треугольнике катет, лежащий против угла 30° равен половине гипотенузы ⇒ гипотенуза AB = 2x км.
3) В ΔDBC ∠BDC = 45° (по условию), ∠DCB = 90°,
тогда ∠DBC = 180° - 90° - 45° = 45°. ⇒ ΔDBC равнобедренный, так как имеет два равных угла ⇒ DC = BC = x км.
4) Тогда в ΔABC сторона AC = x + 0,5 км.
Из ΔABC найти BC можно двумя способами:
I способ. По теореме Пифагора:
Высота горы ≈ 0,683 км ≈ 683 м.
II способ. По теореме синусов, также из ΔABC.
(смотри расчет в I способе).
Высота горы ≈ 0,683 км ≈ 683 м.
Рисунок
Там где написано без названия это 1 способ
Где без названия 2 это 2 способ а 3 это рисунок