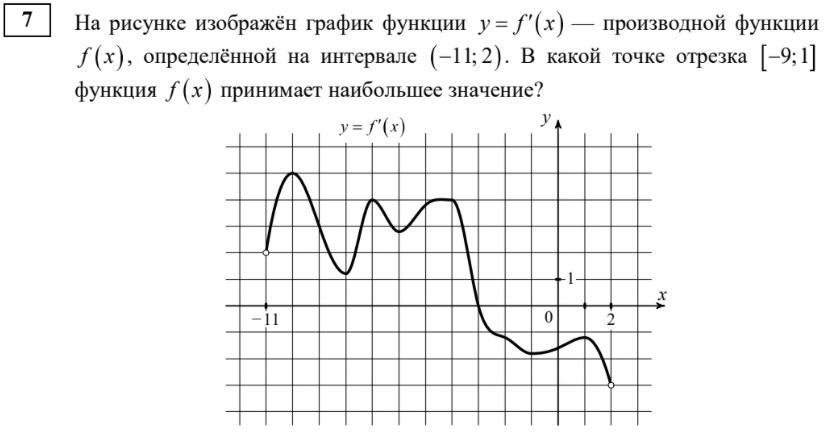
На рисунке изображён график функции y f x = ′ — производной функции f x , определённой на интервале −11; 2 . В какой точке отрезка −9;1 функция f x принимает наибольшее значение?
Ответы
Ответ:
Пошаговое объяснение:
Теорема Ферма (необходимый признак существования экстремума функции)
если точка x₀- точка экстремума функции f(x), то в этой точке производная функции равна нулю (f '(x₀) = 0) или не существует.
мы читаем наоборот. где f '(x₀) = 0 там и экстремум, значит наша точка = (-3; 0)
теперь надо определиться, это максимум или минимум
для этого применим другую теорему
Теорема (первый достаточный признак существования экстремума функции).
критическая точка x₀ является точкой экстремума функции f(x), если при переходе через эту точку производная функции меняет знак, причём, если знак меняется с "плюса" на "минус", то точкой максимума, а если с "минуса" на "плюс", то точкой минимума.
то, что нам надо из этой теоремы, я подчеркнула, потому как у нас производная в точке (-3,0) меняет знак с "+" на "-".
значит это у нас точка точка максимума.
итак, ответ
функция f(x) принимает наибольшее значение в точке (-3; 0)