Пожалуйста, с рисунками и подробным объяснением )

Ответы
Объяснение:
центр описанной окружности в остроугольном и тупоугольном треугольнике - точка пересечения их серединных перпендикуляров.
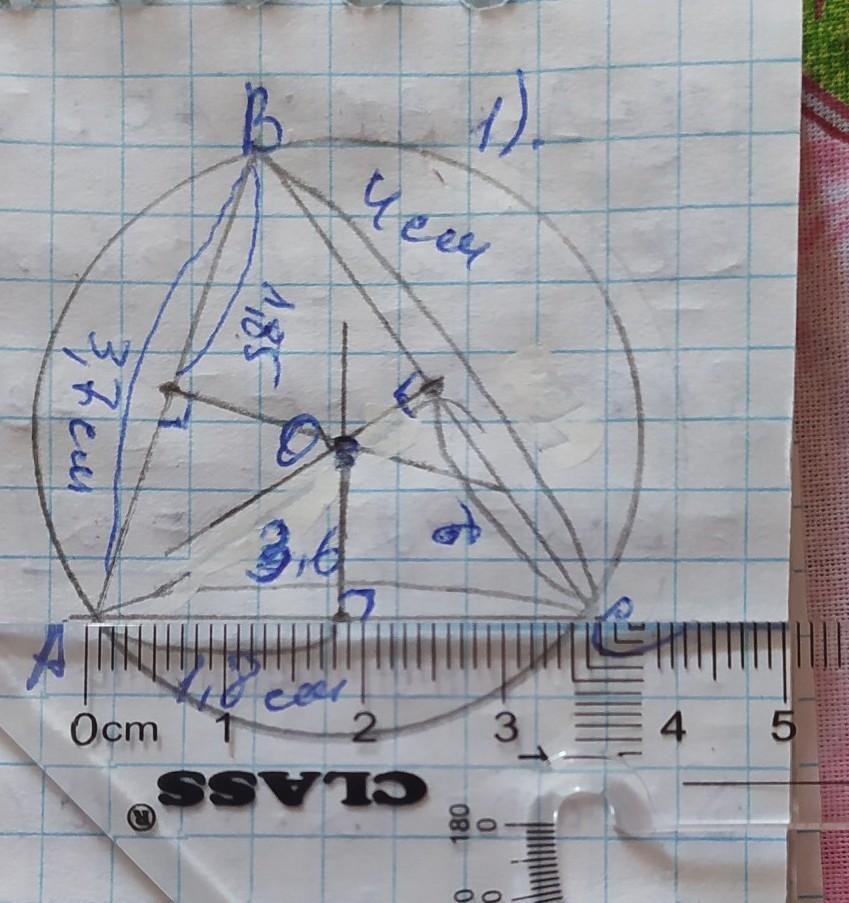
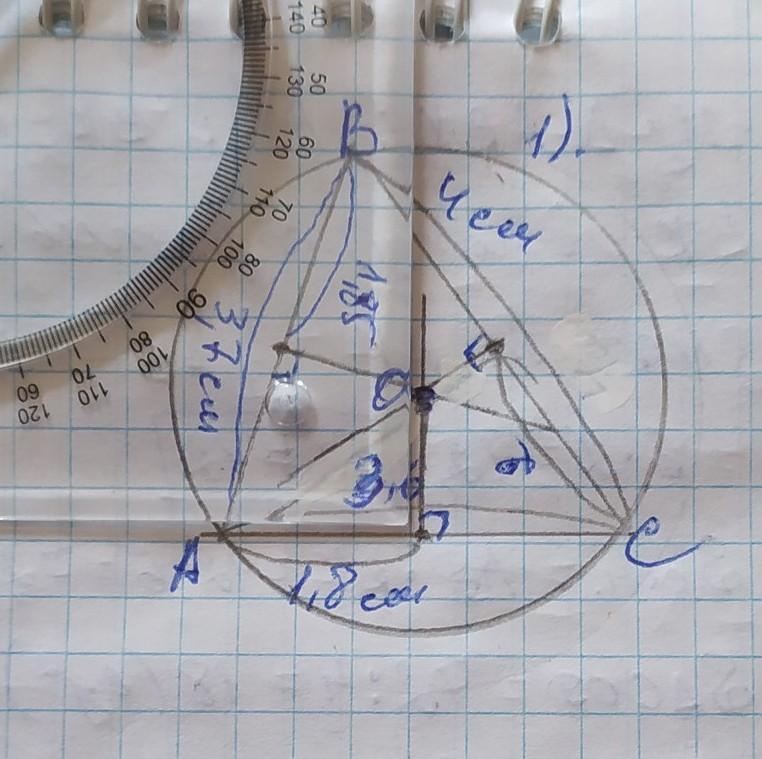
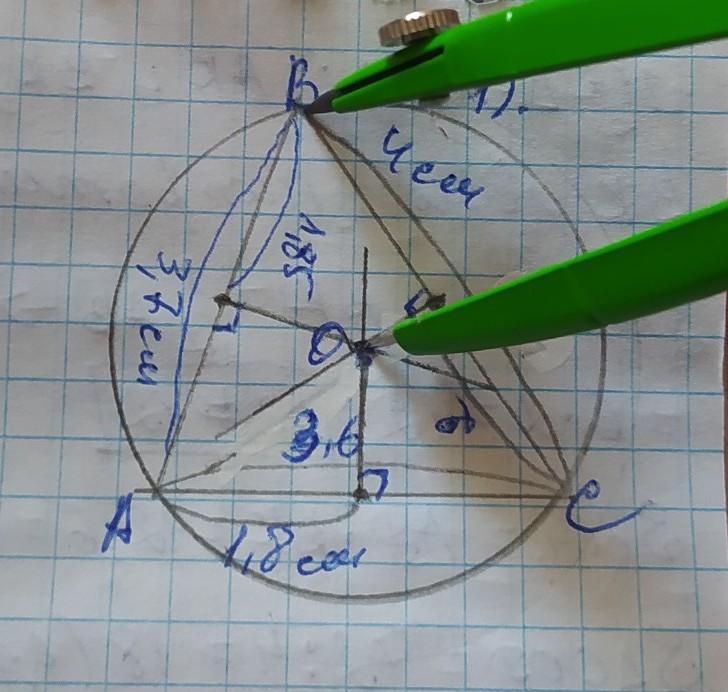
1) Рисуем остроугольный треугольник, измеряем каждую сторону, делим эту величину на 2 и отмечаем точкой середину отрезка. АС=3,6см, значит середина отрезка АС=3,6÷2=1,8см. Отметив эту точку, с помощью угольника проведём к ней перпендикуляр.
Так проделываем с другими двумя сторонами.
Отмечаем точку пересечения перпендикуляров О и фиксируем на ней острую ножку циркуля. Радиус описанной окружности - это расстояние от центра окружности к любой вершине треугольника.
Обозначив радиус, описываем окружность.
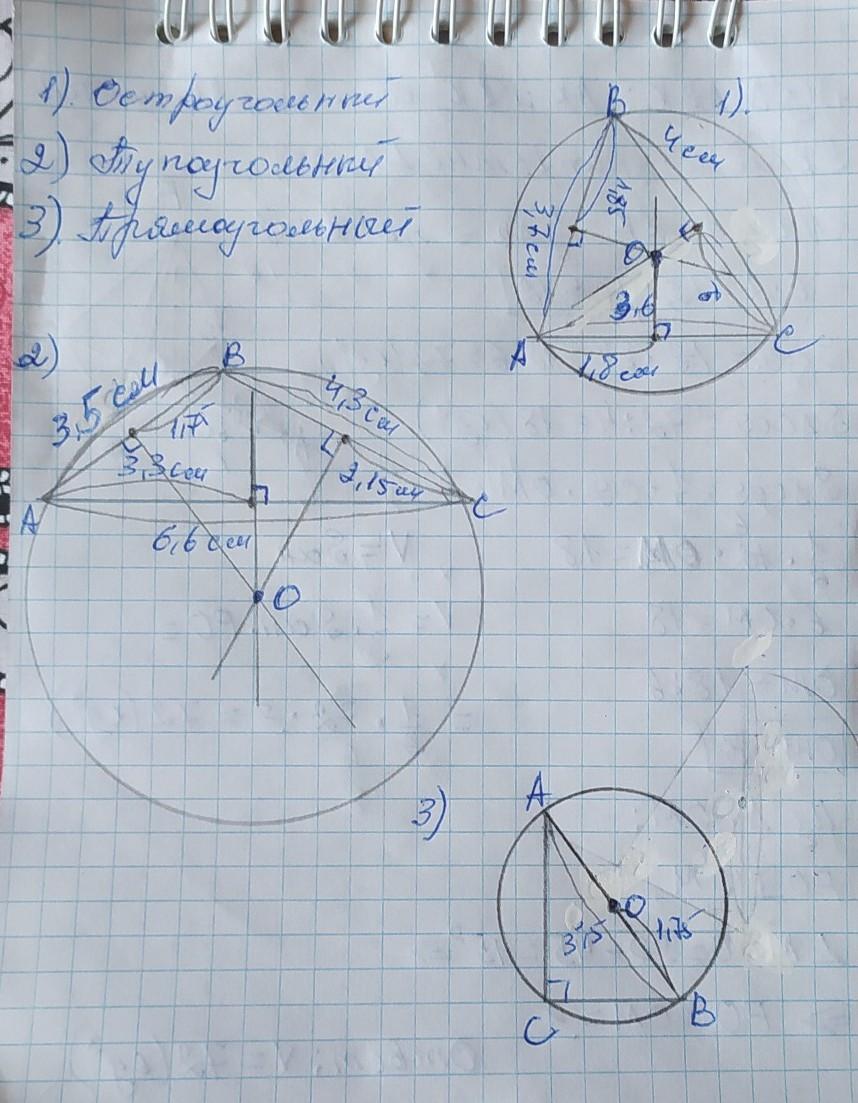
2) То же проделываем с тупоугольном треугольником. Только в тупоугольном треугольнике точка пересечения перпендикуляров находится вне его.
3) В прямоугольном треугольнике центром окружности является середина гипотенузы АВ.
Находим в ней середину по тому же принципу, что и в предыдущих треугольниках и радиусом будет расстояние от центра окружности до любой вершины треугольника. В данном случае гипотенуза равна 3,5см, тогда расстояние от точки О до вершины=3,5÷2=1,75см.