Предмет: Геометрия,
автор: 9lTBOuDPyG
Au_Bis_pret_sm.png
В равнобедренном треугольнике к боковой стороне проведена высота и биссектриса угла, прилежащего к основанию.
Определи угол между высотой и биссектрисой, если угол вершины ∡ B = 10°.
∡ MAN =
°.
Ответы
Автор ответа:
0
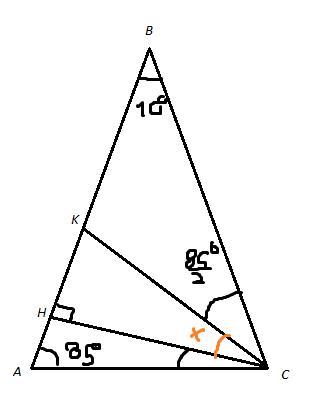
Ответ:
∠KCH = 37,5°
Объяснение:
CK - биссектриса, СН - высота
∠KCH = x
∠В = 10° => ∠A = ∠C = 85°
так как CK - биссектриса ∠KCB = ∠KCA = 42,5°
∠ACH = 180° - ∠HAC - ∠AHC = 5°
∠KCH = ∠KCA - ∠ACH = 42,5° - 5° = 37,5°
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: irinka123380
Предмет: Русский язык,
автор: коста1
Предмет: Русский язык,
автор: comaro00
Предмет: Математика,
автор: ksiusha4