Предмет: Алгебра,
автор: RuslanRussia1881
алгебра срочно помогите пожалуйста
номер 7.77 под номером 1 и 3
Приложения:
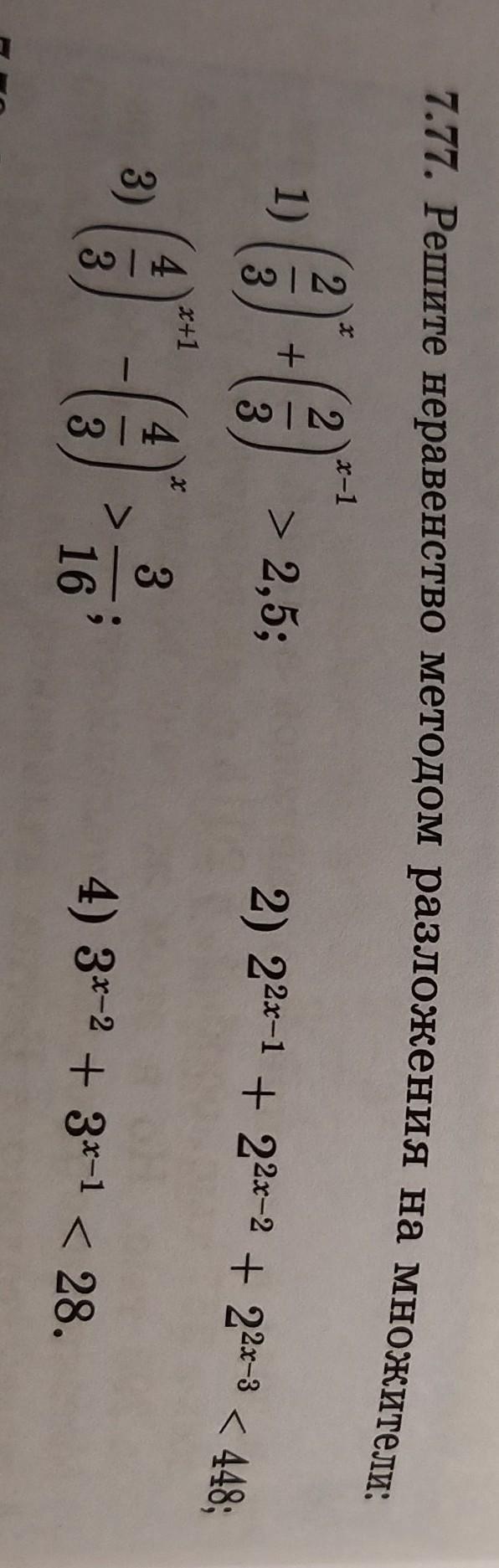
Ответы
Автор ответа:
0
Ответ:
Объяснение:
___________________________
Похожие вопросы
Предмет: Русский язык,
автор: GARYPLAY
Предмет: Русский язык,
автор: Евгения24444
Предмет: Английский язык,
автор: aaaaxex
Предмет: Алгебра,
автор: andrei19790304
Предмет: Биология,
автор: S00S12