Question

30 баллов. Помогите написать ОДЗ к тригонометрическому уравнению. И, если можно, решить его.

Answer 1

Ответ:

$\frac{4 \cos {}^{2} (x) - 3}{ \sqrt{ \frac{1}{3} - \sin(x) } } = 0$

ОДЗ:

$\frac{1}{3} - \sin(x) > 0 \\ \sin(x) < \frac{1}{3} \\ \sin(x) = \frac{1}{3} \\ x = {( - 1)}^{n} arcsin \frac{1}{3} + \pi \: n$

n принадлежит Z.

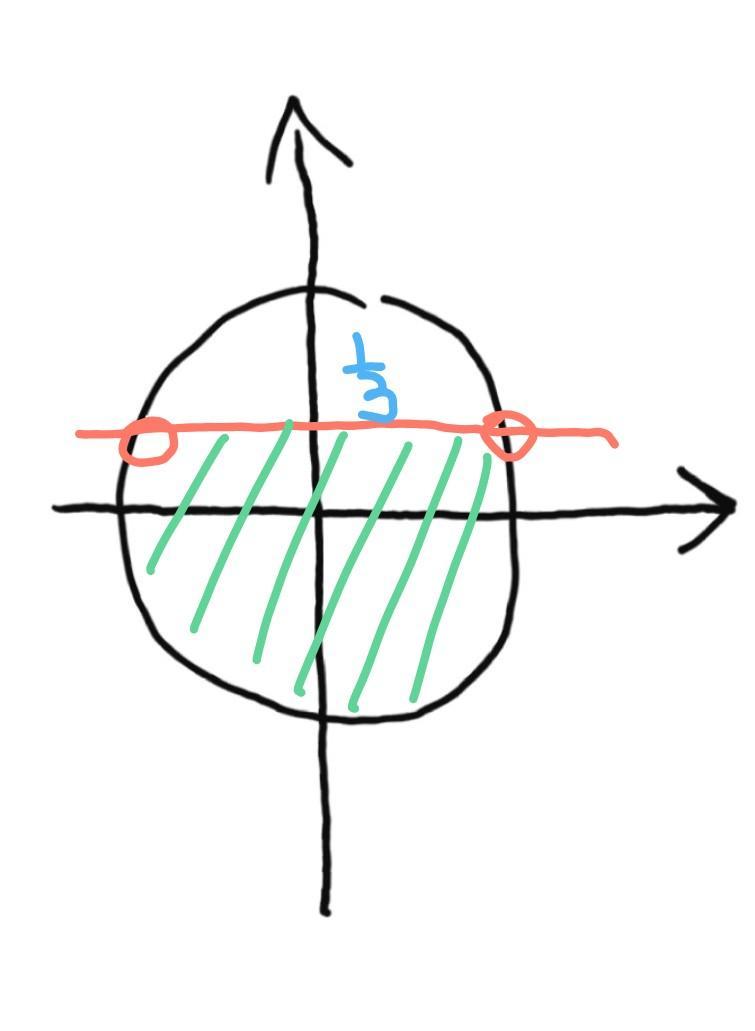
рисунок

$x\in( - \pi - arcsin \frac{1}{3} + 2\pi \: n;arcsin \frac{1}{3} + 2\pi \: n)$

n принадлежит Z.

$\\ 4 \cos {}^{2} (x) - 3 = 0 \\ \cos {}^{2} (x) = \frac{3}{4} \\ \cos(x) = \pm \frac{ \sqrt{3} }{2}$

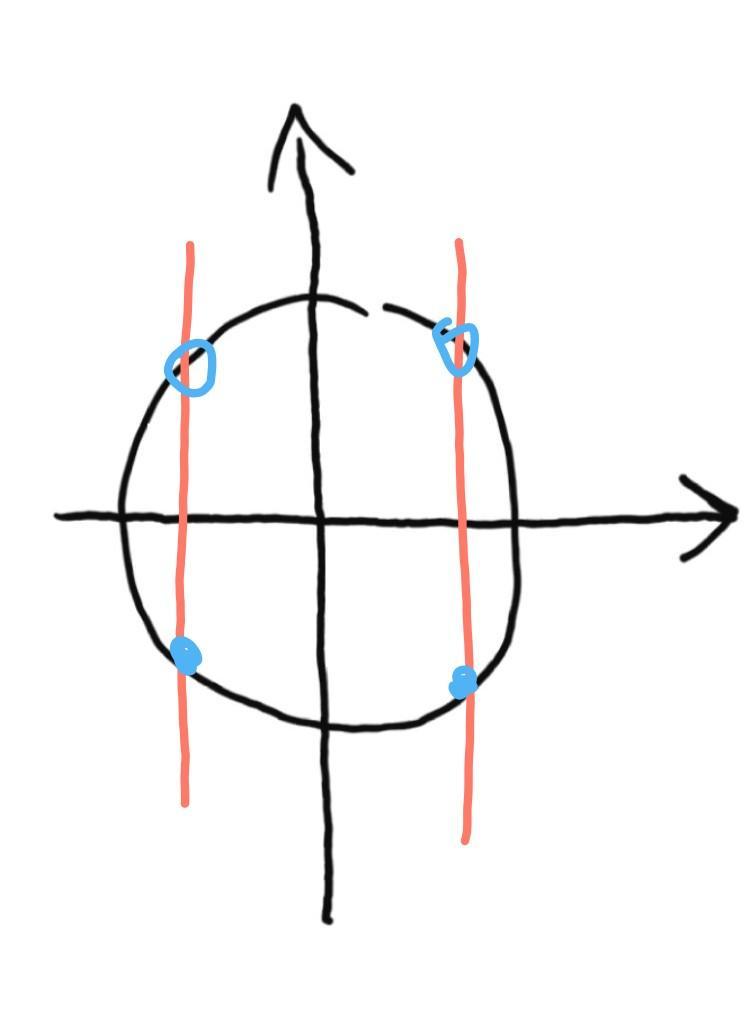
рисунок2

Как видно на рисунке, два корня в верхней части окружности не входят в ОДЗ, поэтому в ответе только два "нижних" корня:

$x1 = - \frac{5\pi}{6} + 2\pi \: n \\ x2 = - \frac{\pi}{6} + 2 \pi \: n$

n принадлежит Z.

б)

[П/6; 3П)

Отберем корни с помощью неравенств:

$x1 = - \frac{5\pi}{6} + 2\pi \: n \\ \\ \frac{\pi}{6} \leqslant - \frac{5\pi}{6} + 2\pi \: n < 3\pi \: \: \: | \times \frac{6}{\pi} \\ 1 \leqslant - 5 + 12n < 18 \: \: \: | + 5 \\ 6 \leqslant 12n < 23 \\ \frac{6}{12 } \leqslant n < 1 \frac{11}{12} \\ \\ n = 1 \\ x1 = - \frac{5\pi}{6} + 2\pi = \frac{7\pi}{6} \\ \\ x2 = - \frac{\pi}{6} + 2 \pi \: n \\ \\ \frac{\pi}{6} \leqslant - \frac{\pi}{6} + 2\pi \: n <3 \pi \\ 1 \leqslant - 1 + 12n < 18 \: \: \: | + 1 \\ 2 \leqslant 12n < 19 \\ \frac{2}{12} \leqslant n < 1 \frac{7}{12} \\ \\ n = 1 \\ x2 = - \frac{\pi}{6} + 2 \pi = \frac{11\pi}{6}$

Ответ: 11П/6; 7П/6.