Предмет: Геометрия,
автор: alexandra4260
Сторона правильного четырехугольника вписанного в окружность с радиусом R равно :....?
С решением пожалуйста)
Ответы
Автор ответа:
5
Ответ:
Что решать то?)
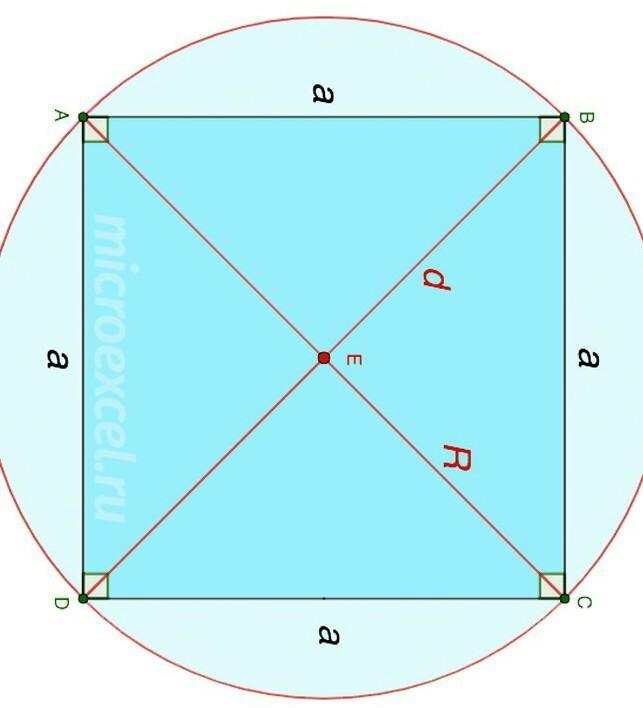
a = R√2, где
a - сторона правильного четырех угольника
R - радиус описанной окружности (треугольник вписан, значит окружность описана)
Если тебе нужен вывод то вот:
1) Строишь квадрат со стороной а.
2) Вокруг квадрата чертешь описаную окружность с радиусом R.
3) Проводишь диаметры так, чтобы вершина угла квадрата и диаметр пересеклись.
3) диаметры = диагоналям (так как окружность описана) => по свойству параллелограмма: диагонали параллелограмма точкой пересечения делятся пополам => d = 2R
4) Так как квадрат - это ещё и ромб => диагонали параллелограмма при пересечении образуют прямой угол => По теореме Пифагора: a= √(R² + R²)= √(2R²)= R√2
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Krasotka3000
Предмет: Технология,
автор: astsakh
Предмет: Русский язык,
автор: дмитревна1
Предмет: Алгебра,
автор: ENJOIKING
Предмет: Русский язык,
автор: kzmail