Question

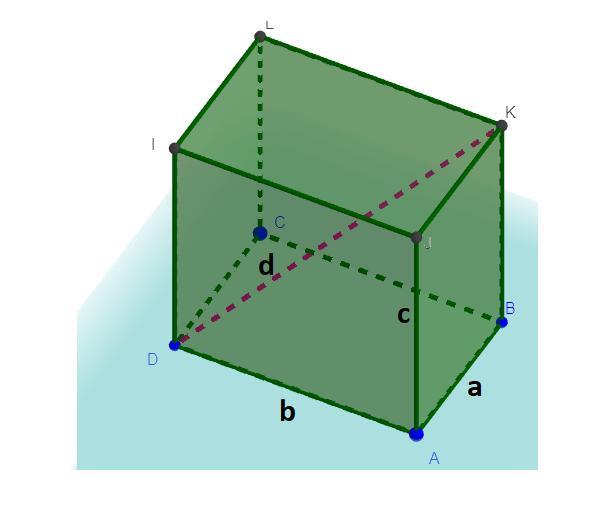
4.Ребро куба равно 4 см. Через диагональ основания под углом в 45° к плоскости основания проведена плоскость, пересекающая боковое ребром. Найдите площадь треугольника DLB. СРОЧНО!!! ДАЮ 35 БАЛЛОВ!!!

Answer 1

Ответ:

2. Объем параллелепипеда 32 кубические единицы

3. Угол между плоскостями 60°

4. SΔDLB = $8\sqrt{2}$ сантиметров квадратных

Объяснение:

2.

Пусть a,b,c - длины различных ребер выходящей из одной вершины. Пусть a = 2, b = 4.Пусть главная диагональ параллелепипеда d, по формуле$d^{2} = a^{2} + b^{2} +c^{2} \Longrightarrow c = \sqrt{d^{2} - a^{2} - b^{2}} = \sqrt{6^{2} - 4^{2} - 2^{2} } = \sqrt{36 - 16 - 4 } = 4$

По формуле объем прямоугольного параллелепипеда это произведение трех различных ребер имеющих общую вершину, тогда V = abc = 2 * 4 * 4 = 32 кубические единицы.

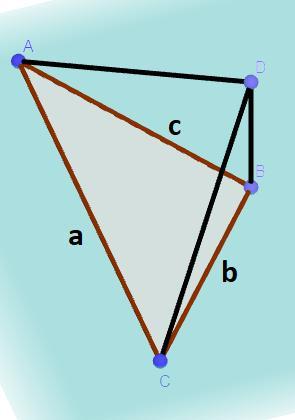
3.

Пусть a,b,c - длины сторон ортогональной проекции треугольника(ΔABC). Пусть a = 39 см, b = 17 см, c = 28 см. Пусть p - полупериметр треугольника ΔABC. p = PΔABC : 2 = (a + b + c) : 2 = (39 + 17 + 28) : 2 = 84 : 2 = 42 см. По формуле Герона для треугольника ΔABC:

$S_{\bigtriangleup ABC} = \sqrt{p(p - a)(p -b)(p - c)} = \sqrt{42(42 - 39)(42 - 17)(42 - 28)} =$

$\sqrt{42 * 3 * 25 * 14} = \sqrt{44100} = 210$ сантиметров квадратных.

S проекции = S * cos α ⇒ α = arccos(S проекции : S) = arccos(210 : 420) =

= arccos(0,5) = 60°.

4.

Пусть ребро куба x, тогда x = 4 см. По формуле площади прямоугольного треугольника SΔCDB = DC * CB * 0,5 = x * x * 0,5 =

x² * 0,5 = 4² * 0,5 = 8 квадратных сантиметров. Так как угол между плоскостью основание и треугольником ΔDBL 45°, то треугольник ΔDBC - ортогональная проекция треугольника ΔDBL.

SΔDBC = SΔDBL * cos α ⇒ SΔDBL = SΔDBC : cos α =  $\dfrac{\dfrac{8}{1} }{\dfrac{\sqrt{2} }{2} } = \dfrac{16 * \sqrt{2} }{\sqrt{2} * \sqrt{2} } = 8\sqrt{2}$ сантиметров квадратных.