Предмет: Геометрия,
автор: syroves
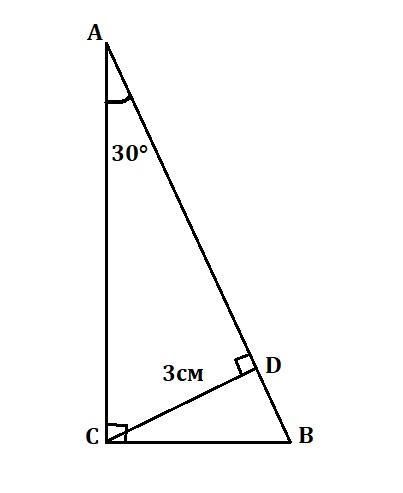
В треугольнике АВС угол С равен 90°,высота СД=3см,острый угол равен 30°.Найди гипотенузу АВ
Ответы
Автор ответа:
0
Ответ:
АВ = 4√3 см
Объяснение:
Дано: ΔАВС(∠С=90°), СD⊥АВ, СD = 3 см, ∠А=30°
Найти: гипотенузу АВ
Рассмотрим ΔАDC.
Так как СD⊥АВ, он прямоугольный, ∠D = 90°.
Катет, лежащего напротив угла в 30° равен половине гипотенузы (свойство):
CD = AC, ⇒ AC = 2· CD = 2 · 3 = 6 cм
Рассмотрим прямоугольный треугольник АВС.
Косинус угла – это отношение прилежащего (близкого) катета к гипотенузе:
см
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Nastushka666
Предмет: Русский язык,
автор: daniev01
Предмет: Русский язык,
автор: Devo2004
Предмет: Математика,
автор: markovajuleta345
Предмет: Математика,
автор: gucciiiii