Предмет: Геометрия,
автор: danilformieenko
стороны треугольника равны 5 см, 12см, 16см. найдите стороны подобного ему треугольника, если коэффициент подобия равен 2
Ответы
Автор ответа:
5
Ответ:
- Стороны треугольника, подобного треугольнику со сторонами 5 см, 12 см, 16 см и коэффициентом подобия 2, равны 10 см, 24 см, 32 см.
Объяснение:
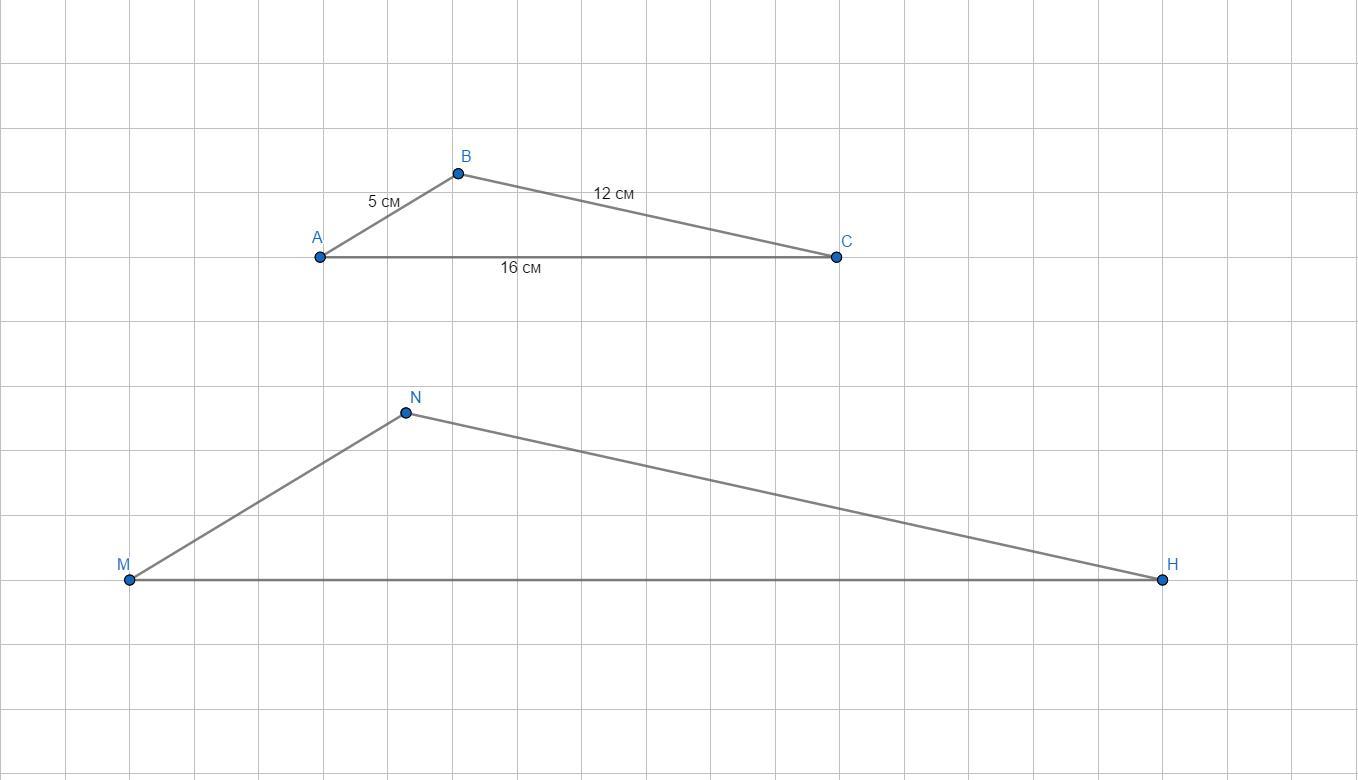
(Изобразим треугольники на чертеже. AB=5 см, BC=12 см, AC=16 см; MN, NH, MH - ?)
- В подобных треугольниках отношения соответствующих линейных элементов пропорциональны и равны коэффициенту подобия k.
По условию , тогда распишем соотношения сторон этих треугольников:
.
Из соотношения:
1) см.
2) см.
3) см.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: центре
Предмет: Английский язык,
автор: вероника771
Предмет: Английский язык,
автор: annaserko
Предмет: Биология,
автор: Аноним
Предмет: Русский язык,
автор: falaleevasof