Предмет: Геометрия,
автор: arlantwink
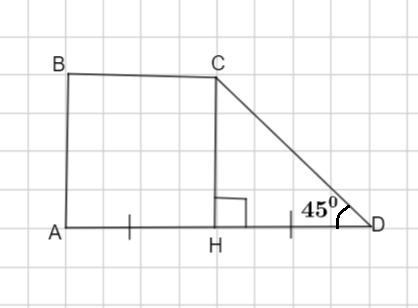
В прямоугольной трапеции ABCD большая боковая сторона равна 10√2 см, а острый угол равен 45 градусов и высота CH делит основание AD пополам. Найдите площадь трапеции.
Ответы
Автор ответа:
1
Ответ:
Площадь трапеции равна 150 см².
Объяснение:
Рассмотрим прямоугольную трапецию ABCD.
см.
∠D=45°. СН - высота и AH=HD
Рассмотрим Δ CHD - прямоугольный и равнобедренный , так как сумма острых углов прямоугольного треугольника равна 90° и если ∠D=45°, то и ∠ DCH =45°. Если два угла в треугольнике равны, то треугольник равнобедренный.
AH=HD=CH =10 см.
Тогда основание AD=AH+HD.
AD=10+10=20 см.
ВС= AH=10 см.
Площадь трапеции можно найти по формуле:
где a и b- основания трапеции, h- высота трапеции.
Значит, площадь трапеции равна 150 см².
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: AlexandI
Предмет: Другие предметы,
автор: alesawww525
Предмет: Английский язык,
автор: ma123ma
Предмет: Геометрия,
автор: вероничка2018
Предмет: Другие предметы,
автор: tomulyaklimenkp0wwah