Question

решить задачу с подробным объяснением

Answer 1

Ответ:

14 + 8√3  ед

Пошаговое объяснение:

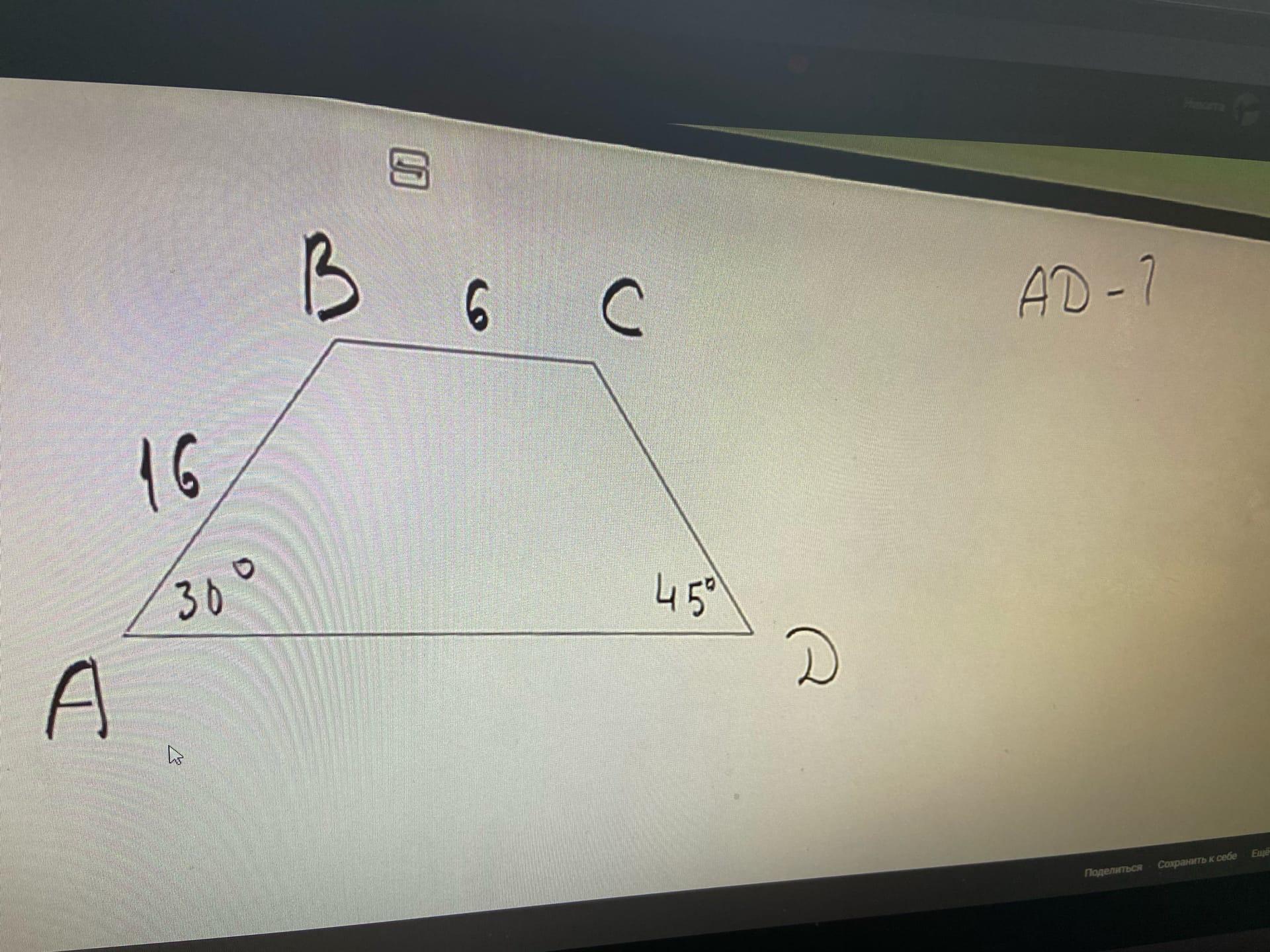
Проведем высоты ВН и СК.

ΔАВН - прямоугольный,  ВН=1/2 АВ = 8 см по свойству катета, лежащего против угла 30°  ВН=СК;

По тореме Пифагора АН=√(АВ²-ВН²)=√(256-64)=√192=8√3.

КН=ВС=6 см.

ΔСDК - прямоугольный, ΔD=45°, значит и ∠КСD=45°, т.к. сумма острых углов прямоугольного треугольника составляет 90°

DК=СК=8.

АD=8√3 + 6 + 8 = 8√3 + 14 ед. изм.

Answer 2

Проведем перпендикуляры ВН и СH₁ к стороне AD ⇒ BC=HH₁=6

ΔАВН - прямоугольный,  ∠A=30°, отсюда BH=16÷2=8 (катет, лежащий против угла 30° равен половине гипотенузы)⇒

По т. Пифагора

$BH^2+AH^2=BA^2\\8^2+AH^2=16^2\\AH^2=16^2-8^2\\AH^2=(16-8)(16+8)\\AH=\sqrt{192} =8\sqrt{3}$

BH=CH₁=8

 

ΔСDH - прямоугольный, ∠D=45°, значит ∠С тоже 45° ⇒ ΔСDH₁ - равнобедренный ⇒

DH₁=СH₁=8

$AD=AH+HH_1+DH_1=8\sqrt{3} +6+8=14+8\sqrt{3}$ ед.

Ответ: AD = 14 + 8√3 ед.

P.S. На рисунке ошибка, вместо CH должно быть CH₁, еще нужно будет на рисунке показать, что CH₁=DH₁ и BC=HH₁