срочно помогите решить систему
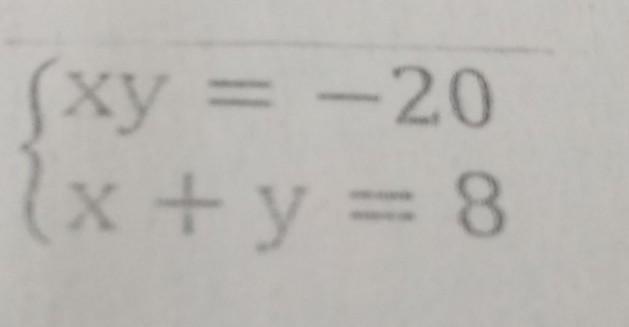
Ответы
Ответ:
{ xy = -20
{ x + y = 8
Выражаем из второго уравнения ( x + y = 8 ) y (нам выразить y легче, чем x, так как он положительный)
{ xy = -20
{ y = 8 - x
Подставляем в выражение xy = -20 вместо y то, что у нас получилось, т.е. 8 - x и решаем это уравнение
x ( 8 - x ) = -20
8x - x² = -20
8x - x² + 20 = 0 (это квадратное уравнение, чтобы было легче его решить, переместим все значения по "стандарту")
-x² + 8x + 20 = 0 ( если что, то a = -1, b = 8, c = 20 )
D = b² - 4ac = 8² - 4 • (-1) • 20 = 144
Находим x по формуле:
и
x1 = -8 + √144 / 2 • (-1) = -8 + 12 / -2 = 4 / -2 х = -2
x2 = -8 - √144 / 2 • (-1) = -8 - 12 / -2 = -20 / -2 = 10
Теперь, зная значения х, найдём значения у:
у = 8 - x
y1 = 8 - x1 = 8 - (-2) = 8 + 2 = 10
y2 = 8 - x2 = 8 - 10 = -2
Составляем координаты, это и будет ответ
Ответ: (-2;10) и (10;-2)
Удачи :)