Предмет: Математика,
автор: marvindedima
Решить задачу Коши ,найти решение дифференциального уравнения
Приложения:
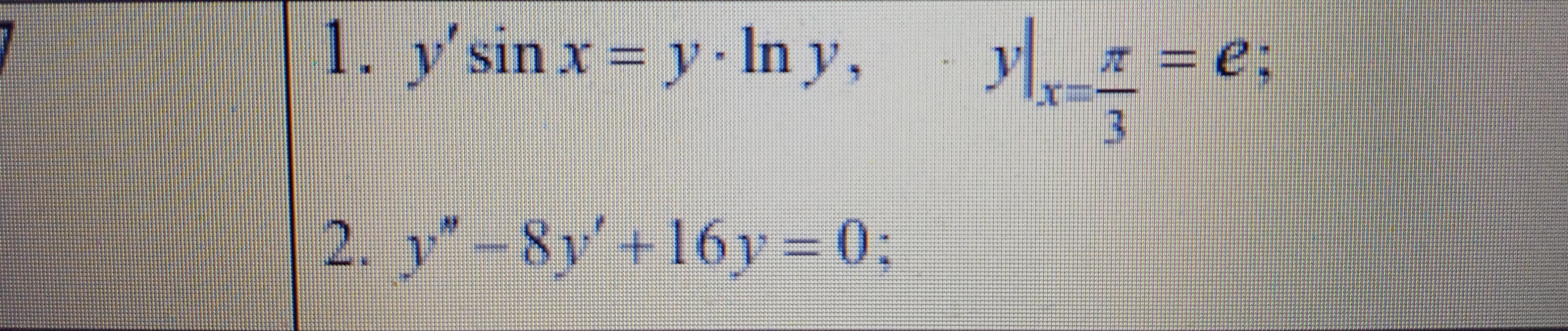
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: пушичка
Предмет: Русский язык,
автор: roxi80
Предмет: Технология,
автор: baligma
Предмет: Английский язык,
автор: LJкрасотка200711
Предмет: Алгебра,
автор: Aluashka111