Question

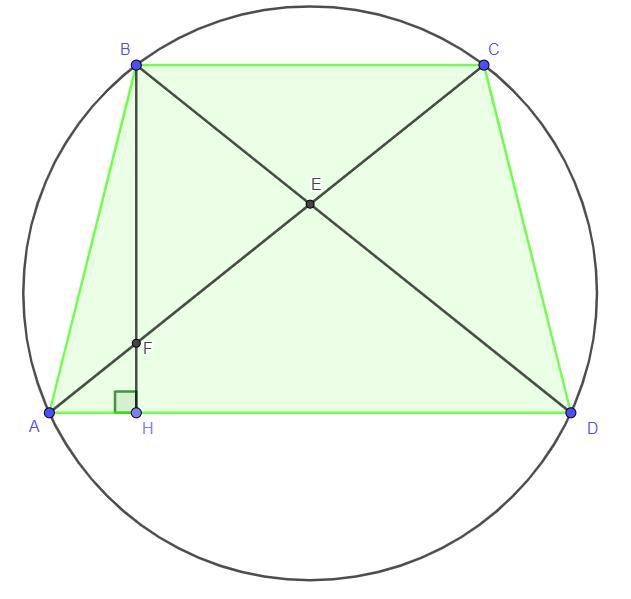
В окружность радиуса 5 вписана трапеция ABCD диагонали которой взаимно перпендикулярны, и большее основание AD = 8. Найти меньшее основание, боковую сторону и площадь трапеции.

Answer 1

Ответ:

$AB = CD = 5\sqrt{2}$

$BC = 6$

$S_{ABCD} = 49$

Объяснение:

Дано: ABCD - вписанная в окружность трапеция, AD = 8, R = 5, AC ⊥ BD

Найти: AB, CD, BC, $S_{ABCD}$ - ?

Решение: По теореме если вокруг трапеции можно описать окружность, то трапеция равнобедренна, следовательно трапеция ABCD - равнобедренная. Проведем высоту из точки B в точку H на основание AD. Пусть BH ∩ AC = F и AC ∩ BD = E. Рассмотрим прямоугольный треугольник ΔAED. Угол ∠EAD = ∠EDA, так как эти опираются на хорды СВ и AB соответственно, так как трапеция ABCD - равнобедренная, то AB = CD и углы опирающиеся на эти хорды, тоже равны. Так как треугольник ΔAED и равнобедренный, то по свойствам равнобедренного прямоугольного треугольника его углы 45°. По свойствам трапеции треугольник ΔAED подобен ΔBEC, следовательно углы этих треугольников равны и ∠EBC = ECB = 45°. Треугольник ΔAFH подобен треугольнику ΔBFC по двум углам, так как ∠AFH = ∠BFC как вертикальные углы, а ∠CAD = ∠ACB как внутренние разносторонние углы при параллельных прямых при секущей по теореме (AD║BC - по определению трапеции). Рассмотрим треугольник ΔBFC, так как ∠ECB = 45° и BH ⊥ BC по свойствам высоты трапеции, то треугольник ΔBFC - равнобедренный, тогда BF = BC. Так как треугольник ΔAFH подобен треугольнику ΔBFC, то треугольник ΔAFH - тоже равнобедренный и

AH = HF. По свойствам равнобедренной трапеции AH = (AD - BC)*0,5.

BH = BF + FH = BC + AH =  BC + (AD - BC)*0,5 = (BC + AD)*0,5. Радиус описанной окружности около трапеции ABCD совпадает с радиусом описанной окружности около треугольника ABD. По формуле радиуса описанной окружности.

$R = \frac{AB}{2 * \sin \angle BDA} \Longrightarrow AB = 2R\sin\angle BDA = 2 * 5 * \sin45^{\circ} = \frac{10\sqrt{2} }{2} = 5\sqrt{2}$ .

Рассмотрим треугольник ΔBAH. По теореме Пифагора:

$AB^{2} = AH^{2} + BH^{2}$

$(5\sqrt{2} )^{2} = (\frac{AD - BC}{2})^{2} + (\frac{AD + BC}{2})^{2}$

$50 = \frac{AD^{2} - 2BC * AD + BC^{2} + AD^{2} + 2AD * BC + BC^{2}}{4}|*4$

$200 = 2AD^{2} + 2BC^{2}|:2$

$100 = AD^{2} + BC^{2}$

$BC = \sqrt{100 - AD^{2}} = \sqrt{100 - 8^{2} } = \sqrt{100 - 64} = \sqrt{36} = 6$

По формуле площади трапеции:

$S_{ABCD} = (\frac{BC + AD}{2}) * BH =(\frac{BC + AD}{2})^{2} = (\frac{6 + 8}{2})^{2} = 7^{2} = 49$.

$AB = CD = 5\sqrt{2}$