Question

Если магнитный кубик массой 4 кг примагнитить к вертикальному железному листу и чуть-чуть толкнуть его вниз, то он будет сползать с постоянной скоростью 2 м/с. Если тот же магнит положить на такой же железный лист и тянуть вдоль листа, то возникнет сила трения, равная 60 Н. Чему равна сила магнитного притяжения кубика к листу?

Answer 1

Ответ:

Объяснение:

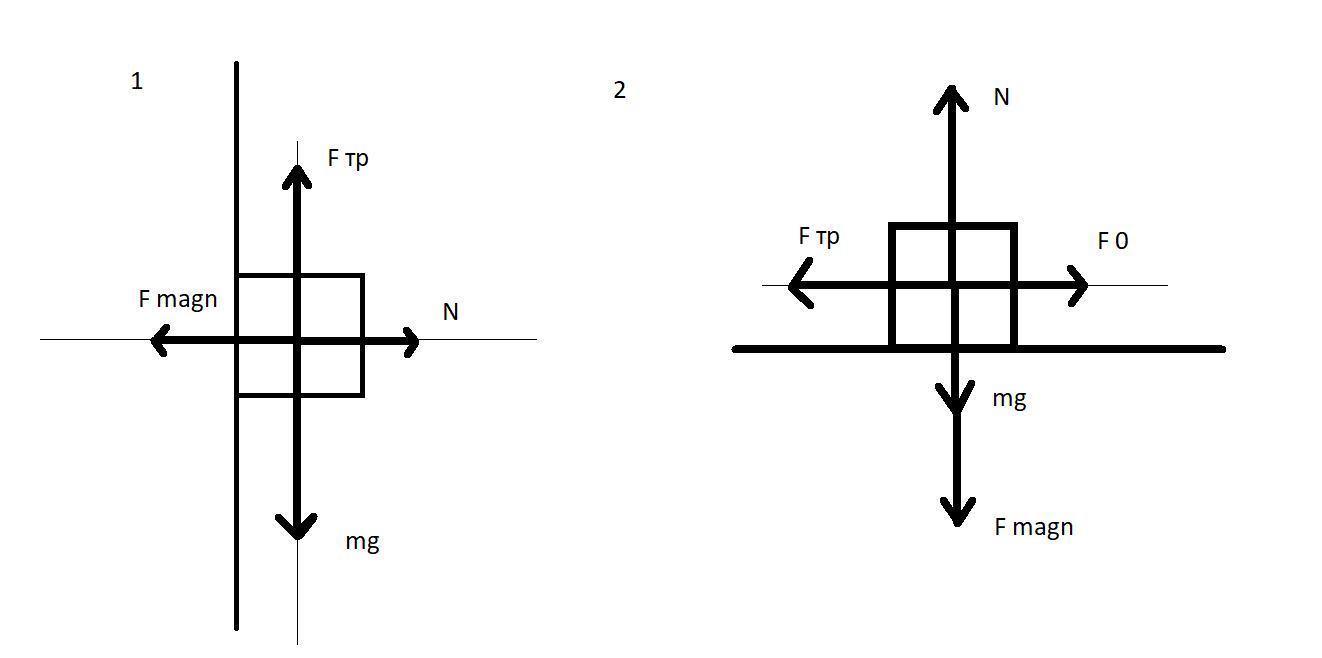
Рассмотрим 1 случай и запишем действующие силы. Так как кубик движется с постоянной скоростью сумма сил равна 0:

$m\vec{g} + \vec{F}_{magn} + \vec{N} + \vec{F}_{fr} = 0$

По осям:

$\begin{cases}mg = F_{fr}\\F_{magn} = N\end{cases} \Rightarrow\begin{cases}mg = \mu N\\F_{magn} = N\end{cases} \Rightarrow mg = \mu F_{magn} (*)$

Рассмотрим второй случай. Сила F0 - сила тяги равная силе трения. Рассмотрим силу трения.

$\begin{cases}F_{fr} = \mu N\\mg + F_{magn} = N\end{cases} \Rightarrow F_{fr} = \mu (mg + F_{magn}) (**)$

Выражая $\mu$ из (*) и (**) получим

$\begin{cases}\mu = \dfrac{mg}{F_{magn}}\\\mu = \dfrac{F_{fr}}{mg + F_{magn}}\end{cases} \Rightarrow \dfrac{mg}{F_{magn}} = \dfrac{F_{fr}}{mg + F_{magn}}\\ \Rightarrow (mg + F_{magn})mg = F_{fr}F_{magn}\Rightarrow (mg)^2 = F_{fr}F_{magn} - F_{magn}mg \Rightarrow \\\Rightarrow (mg)^2 =F_{magn} (F_{fr} - mg) \Rightarrow F_{magn} = \dfrac{(mg)^2}{F_{fr} - mg} = \dfrac{(4 *10)^2}{60 - 4 * 10} = 80~N$