Предмет: Математика,
автор: Аноним
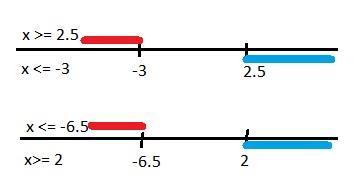
Решите систему неравенств
Приложения:

Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
не пересекаются не пересекаются
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: 34567893
Предмет: Алгебра,
автор: SOBOS569
Предмет: Русский язык,
автор: ggdegsegs762
Предмет: Математика,
автор: tatyanacherkas2
Предмет: Алгебра,
автор: 921