ПОМОГИТЕ СРОЧНО ДАЮ 50 БАЛЛОВ

Ответы
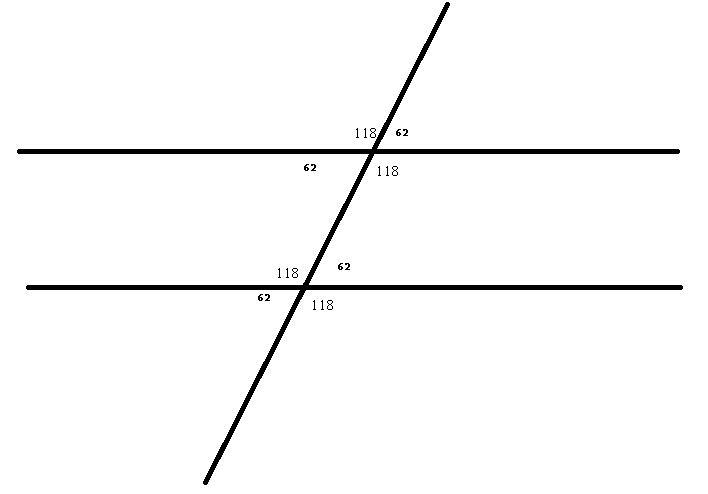
1. Предположим, что один из поперечных углов равен 62^o(во всех других вариантах ответ будет тем же из за параллельности прямых).
<AOD поперечен <ODE => <ODE = 62^o => <GDF = 62^o(так как <GDF == <ODE).
<AOD == <BOC => <BOC = 62^o.
<AOB == <COD => <AOB = (360-(62+62))/2 = 118^o => <BOC = 118^o.
Одни и те же действия с <GDO & <FDE.
Тоесть у нас есть углы, которые с самого начала определены.
У этих двух параллельных прямых есть 2 определения углов — 62^o & 118^o, что и означает, что угол 108 градусов не может быть.(Во второй картинке всё показано).
2. Дано 2 прямых — FB и AE, надо доказать, что FB || AE.
Прямая FE — пресекает FB и AE, данные нам углы — <1, и <2 — равны друг другу, также считаются поперечными углами.
А по 1-ому признаку параллельности прямых — поперечные углы равны, тоесть FB || AE.
3. Легче лёгкого.
Так как прямые параллельны, то соответсвующие углы равны друг другу(по 2-ому признаку параллельности прямых).
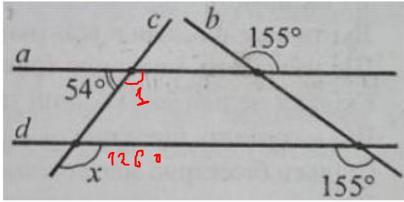
<1 параллелен углу x.
<1 = 180-54 => <1 = 126^o.
<1 == <x => <x = 126^o. (Смотри первую картинку).
Мы конечно можем найти <x более сложным путём, но разве надо?