Предмет: Алгебра,
автор: tentigenovsyjmyk
Решите дифференциальное уравнение
Приложения:
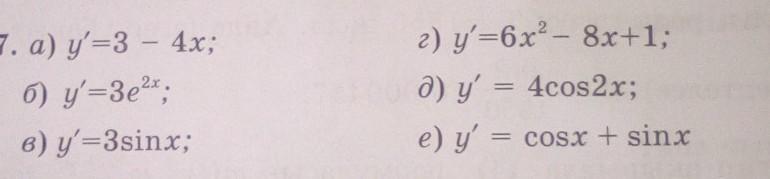
Ответы
Автор ответа:
2
Ответ:
а
б
в
г
д
е
Похожие вопросы
Предмет: Математика,
автор: irenam23
Предмет: Математика,
автор: ayseltural
Предмет: Математика,
автор: m241
Предмет: Математика,
автор: Тимурчан
Предмет: История,
автор: Заяц167