Предмет: Алгебра,
автор: 87770546011
ребят помогите пожалуйста с алгеброй. а то дома сижу больной не знаю как это делать.
Приложения:
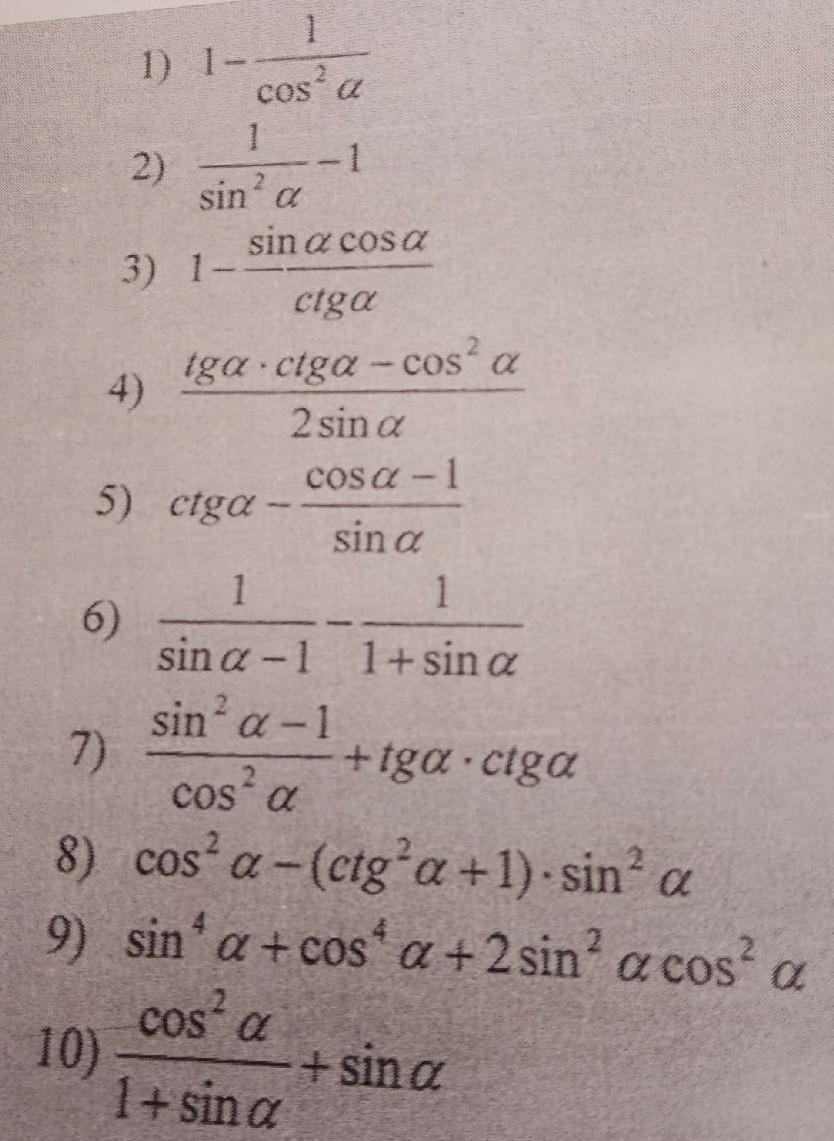
Ответы
Автор ответа:
1
Ответ:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
87770546011:
спасибо
Автор ответа:
0
Ответ:
решение смотри на фотографии
Объяснение:
Приложения:




Похожие вопросы
Предмет: Химия,
автор: aikenbeiker
Предмет: Алгебра,
автор: imthepussyslayer
Предмет: Русский язык,
автор: masha5500
Предмет: Математика,
автор: катя5281
Предмет: Русский язык,
автор: Шайбы