Предмет: Алгебра,
автор: Аноним
СРОЧНО! ПОЖАЛУЙСТА, ПОМОГИТЕ!!!
Приложения:
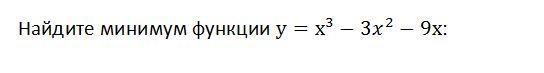
Ответы
Автор ответа:
0
Объяснение:
Найдем первую производную функции
Приравняем ее к нулю
Найдем корни получившегося уравнения
Вычислим значения функции
Используем достаточное условие экстремума функции одной переменной.
Найдем вторую производную
точка точка максимума функции
точка точка минимума функции
Похожие вопросы
Предмет: Математика,
автор: Ksenia121932261
Предмет: Математика,
автор: Валерия1605
Предмет: Алгебра,
автор: Vitalikkrio
Предмет: Русский язык,
автор: ptis19781
Предмет: Английский язык,
автор: mariaklueva