Предмет: Алгебра,
автор: polinamuhovikova
ПРОШУ ВАС ПОМОГИТЕ ПОЖАЛУЙСТА!!!
ОТМЕЧУ ВАШ ОТВЕТ КАК ЛУЧШИЙ!!!!
Приложения:
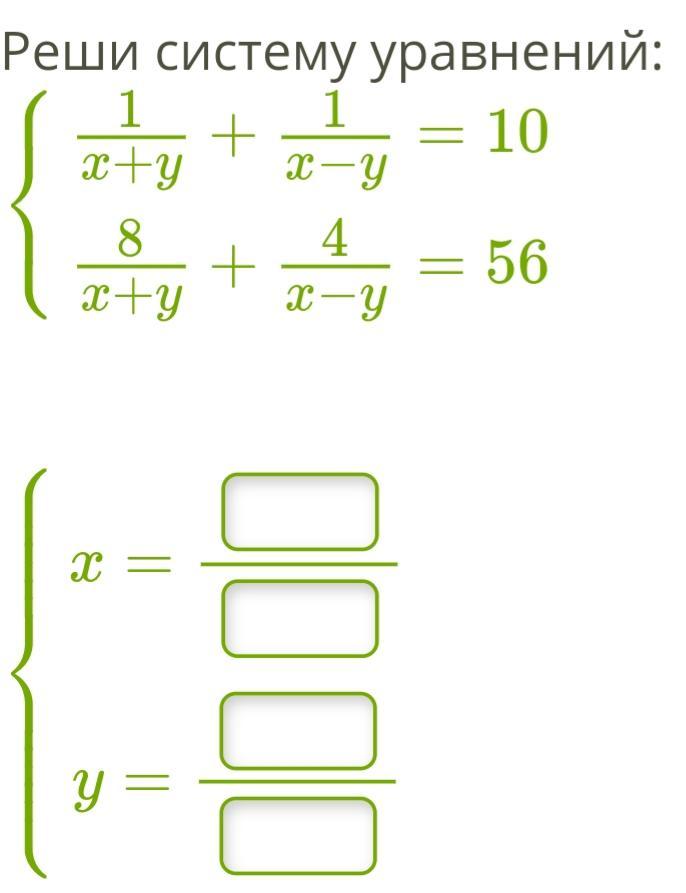
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Физика,
автор: nissanlove
Предмет: Математика,
автор: green2224
Предмет: Химия,
автор: valeriya2314
Предмет: Математика,
автор: ксюшакот4
Предмет: Алгебра,
автор: Thegrishsa