Предмет: Математика,
автор: Аноним
50 баллов. решить дифференциальное уравнение высшего порядка (на фото тоже есть) спасибо
y’’’=1/3sin7x+4x^3
Приложения:
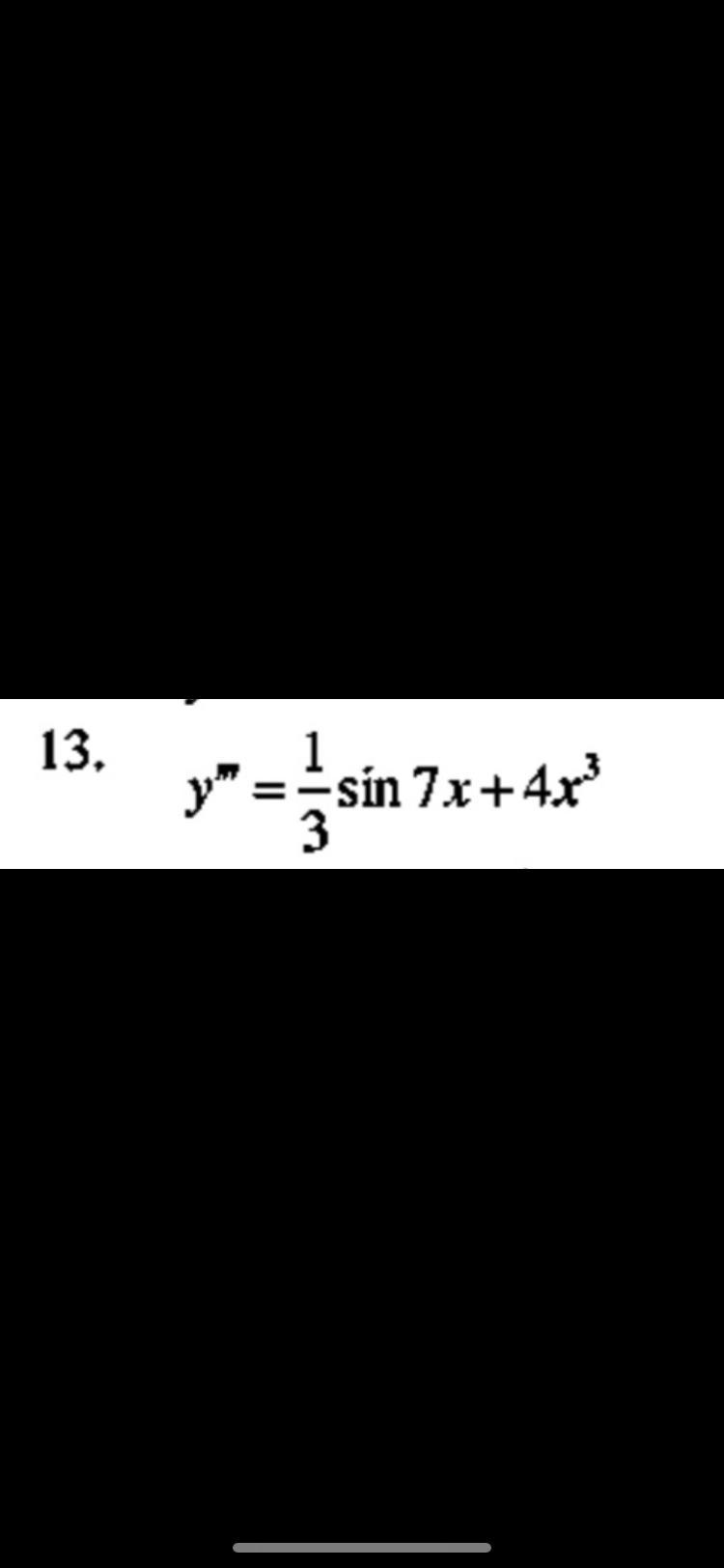
Ответы
Автор ответа:
1
Ответ:
общее решение
Аноним:
спасибо))
Похожие вопросы
Предмет: Математика,
автор: kamkin1998
Предмет: Математика,
автор: 2347618978962420
Предмет: Геометрия,
автор: Кане
Предмет: Русский язык,
автор: belosludtzevaa
Предмет: Окружающий мир,
автор: Pharik