Question

Постройте график функции y=х²-4x+3
опишите его свойства по алгоритму
1 Область определения функции. D(y)
2 Область значения функции E(y)
3.Нули функции ( аргумент точек пересечения параболы с осью ОХ) 4.Знакопостоянство ( какая часть параболы находится выше оси ОХ у>0 , какая часть параболы находится ниже оси ОХ у<0)
5 Наибольшее (наименьшее) значение функции ( значение ординаты вершины параболы)
6.Промежутки возрастания (убывания ) функции

Answer 1

Ответ:

$y=x^2-4x+3$  - графиком функции является парабола

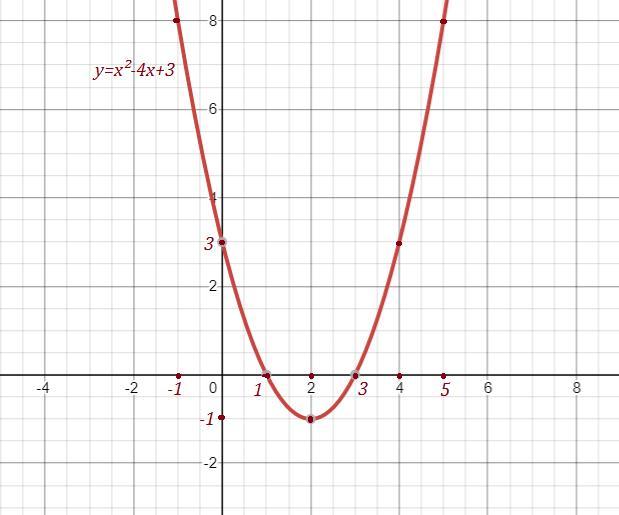
Вершина в точке (2,-1) , ветви направлены вверх .   проходит через точки  (-1,8) , (5,8) , (4,3) , (1,0) (3,0) .

$1)\ \ \ D(y)=(-\infty ;+\infty )\\\\2)\ \ E(y)=[\ -1\ ;\, +\infty\ )\\\\3)\ \ x_1=1\ ,\ x_2=3\\\\4)\ \ y>0\ x\in (-\infty \ ;\ 1\ )\cup (\ 3\ ;+\infty \, )\\\\{}\ \ \ \ \ y<0:\ x\in (\ 1\ ;\ 3\ )\\\\5)\ \ y_{min}=y(2)=-1\\\\6)\ \ y\ \nearrow vozrastzet\ :\ x\in [\ 2\ ;+\infty\, )\\\\{}\ \ \ \ \ y\ \searrow\ ybuvaet\ :\ x\in (-\infty \, ;\ 2\ ]$

Answer 2

Ответ:

В решении.

Объяснение:

График функции - парабола со смещённым центром.

                Таблица:

х   -2   -1   0   1    2   3   4   5   6

у   15   8   3   0   -1   0   3   8   15

График прилагается.

1. Область определения функции. Ничем не ограничена.

D(y)  = х∈(-∞; +∞).

2. Область значения функции E(y). Ограничена ординатой вершины параболы у = -1.

E(y) = у∈[-1; +∞).

3. Нули функции ( аргумент точек пересечения параболы с осью Ох).

х = 1;  х = 3. Координаты точек (1; 0);  (3; 0).

4. Знакопостоянство ( какая часть параболы находится выше оси Ох у>0, какая часть параболы находится ниже оси Ох у<0)

а) у>0 при х∈(-∞; 1)∪(3; +∞);

б) у<0 при х∈(1; 3).

5. Наибольшее (наименьшее) значение функции ( значение ординаты вершины параболы)

.

а) у наиб. не существует.

б) у наим. = -1.

6. Промежутки возрастания (убывания ) функции.

а) функция возрастает на промежутке х∈[2; +∞);

б)  функция убывает на промежутке х∈(-∞; 2].

cddff3840a4f5eef4d99c6a8a76271bb.docx