Предмет: Алгебра,
автор: smurfio
Найти производную функцию
Приложения:
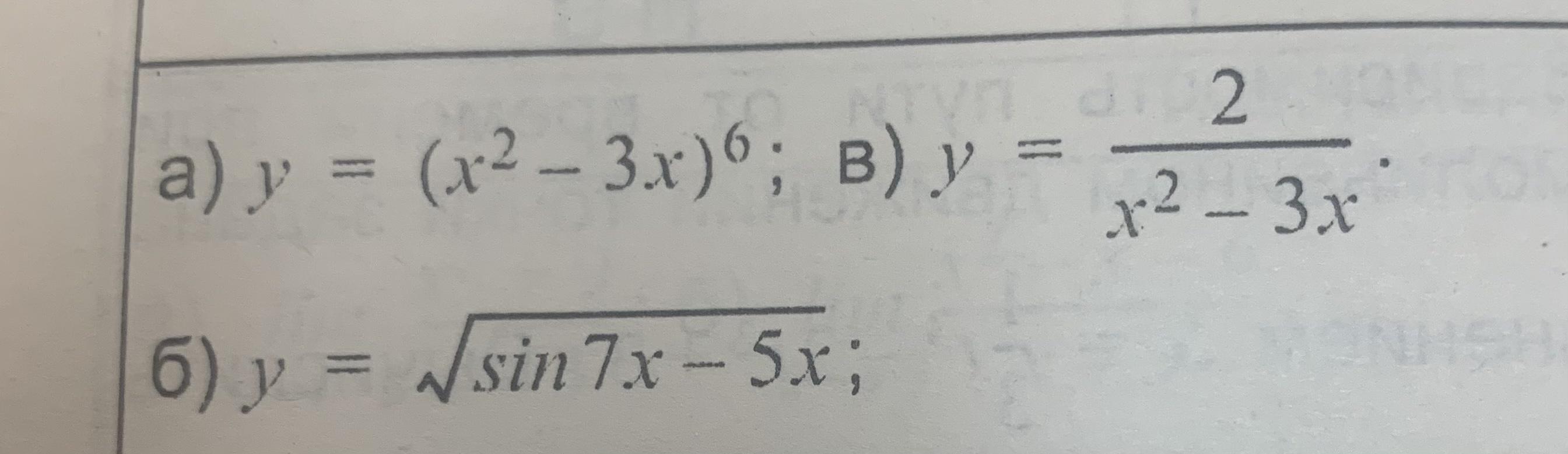
Ответы
Автор ответа:
0
Ответ:
а
б
в
Похожие вопросы
Предмет: Русский язык,
автор: Vanyukha564
Предмет: Геометрия,
автор: Volodya116
Предмет: Математика,
автор: zagidovasaidat
Предмет: Алгебра,
автор: ксю795
Предмет: Геометрия,
автор: nastz45678