Предмет: Математика,
автор: dimagunko08
⦁ Даны точки A(‒1,5) и B(‒7,1). Найдите:
⦁ длину отрезка AB;
⦁ расстояние от точки А до точки В1, координата которой противоположна координате точки В;
⦁ определите координаты точек, делящих отрезок АВ на четыре равные части.
Ответы
Автор ответа:
5
Нужно знать:
1) длину отрезка АВ, если А(х₁) и В(х₂) находят по формуле: АВ = |х₂ - х₁|;
2) координаты середины отрезка АВ находят по формуле: х = (х₁ + х₂)/2.
Поэтому:
1) найдем длину отрезка AB, если A(-1,5) и B(-7,1):
АВ = |-1,5 - (-7,1)| = |-1,5 + 7,1| = |5,6| = 5,6;
2) расстояние от точки А до точки В₁, координата которой противоположна координате точки В:
B₁(7,1), тогда АВ₁ = |-1,5 - 7,1| = |-8,6| = 8,6;
3) определим координаты точек, делящих отрезок АВ на четыре равные части:
середина АВ - точка С₁ имеет координату (-1,5 + (-7,1))/2 = -8,6/2 = -4,3;
середина АС₁ - точка С₂ имеет координату (-1,5 + (-4,3))/2 = -5,8/2 = -2,9;
середина ВС₁ - точка С₃ имеет координату (-7,1 + (-4,3))/2 = -11,4/2 = -5,7.
Приложения:
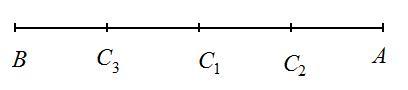
Похожие вопросы
Предмет: Математика,
автор: Дарья12111
Предмет: Математика,
автор: mazunina1993
Предмет: Математика,
автор: kseniyasheb
Предмет: История,
автор: Ясмин07
Предмет: Физика,
автор: Bubadog