Предмет: Алгебра,
автор: AHTOIIIKA75
помогите решить пределы , хоть одно из 3 , плиз очень срочно надо .
ТОлько с помощью замечательных пределов , методом ЛОпиталя не нужно .
Только 18 вариант
Приложения:
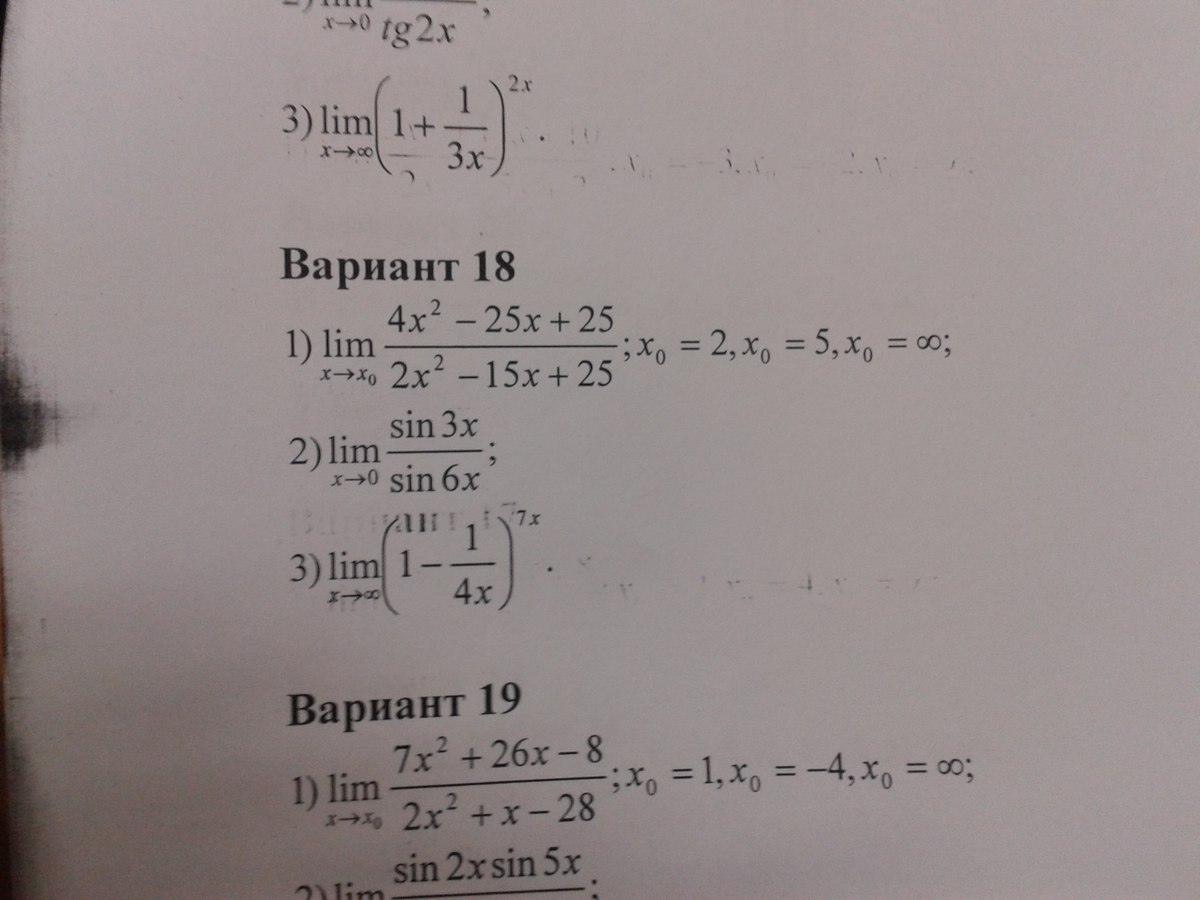
Ответы
Автор ответа:
0
1) Вначале упростим выражение, стоящее в пределе:
4x^2 - 25x + 25 = 4*(x - 5/4)(x - 5) = (4x - 5)(x - 5)
2x^2 - 15x + 25 = 2*(x - 5/2)(x - 5) = (2x - 5)(x - 5)
(4x - 5)(x - 5) / (2x - 5)(x - 5) = (4x - 5)/(2x - 5)
теперь нужно просто подставить значения x0 в выражения и найти предел:
x0 = 2, lim(x->2) ((4*2 - 5)/(2*2 - 5)) = -3
x0 = 5, lim(x->5) ((4*5 - 5)/(2*5 - 5)) =3
x0 = бесконечность, lim(x->бесконечность) ((4*(бесконечность) - 5)/(2*(бесконечность) - 5)) = 2
2) lim(x->0)(sin(3x) / sin(6x)) = 0.5*lim(x->0)(1/ cos(3x)) = 0.5
3) lim(x-> бесконечность)(1 - 1/(4x))^7x) = выделяем второй замечательный предел = lim(x-> бесконечность)((1 - 1/(4x))^4x))^7/4) = e^(7/4)
4x^2 - 25x + 25 = 4*(x - 5/4)(x - 5) = (4x - 5)(x - 5)
2x^2 - 15x + 25 = 2*(x - 5/2)(x - 5) = (2x - 5)(x - 5)
(4x - 5)(x - 5) / (2x - 5)(x - 5) = (4x - 5)/(2x - 5)
теперь нужно просто подставить значения x0 в выражения и найти предел:
x0 = 2, lim(x->2) ((4*2 - 5)/(2*2 - 5)) = -3
x0 = 5, lim(x->5) ((4*5 - 5)/(2*5 - 5)) =3
x0 = бесконечность, lim(x->бесконечность) ((4*(бесконечность) - 5)/(2*(бесконечность) - 5)) = 2
2) lim(x->0)(sin(3x) / sin(6x)) = 0.5*lim(x->0)(1/ cos(3x)) = 0.5
3) lim(x-> бесконечность)(1 - 1/(4x))^7x) = выделяем второй замечательный предел = lim(x-> бесконечность)((1 - 1/(4x))^4x))^7/4) = e^(7/4)
Похожие вопросы
Предмет: Русский язык,
автор: ermenbay186
Предмет: Химия,
автор: ulianaknizeva11
Предмет: Обществознание,
автор: polina20071114
Предмет: Алгебра,
автор: chechengirl