Предмет: Математика,
автор: Vikiviki1979
Найти частное решение дифференциального уравнения
Приложения:
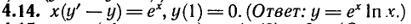
Ответы
Автор ответа:
1
Ответ:
Это ЛДУ
Замена:
общее решение
частное решение
Похожие вопросы
Предмет: География,
автор: dimaglushko1
Предмет: Физика,
автор: gayagalustyan
Предмет: Русский язык,
автор: roza55555
Предмет: Математика,
автор: viktoriyasuhor